Генри Дьюдени - Пятьсот двадцать головоломок

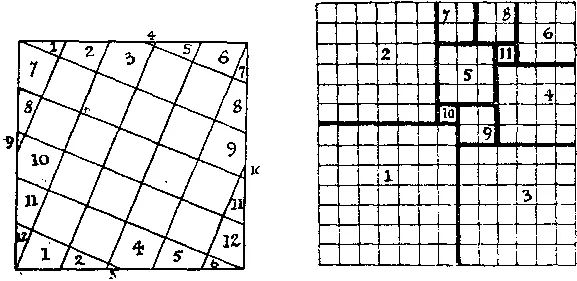
336. По-видимому, существует лишь одно решение этой головоломки, которое представлено на рисунке справа. Наименьшее число частей равно 11; они должны иметь указанные размеры. Три наибольшие части не могут располагаться иначе, а группу из восьми квадратов можно «отразить».

[По поводу общей задачи, так и не решенной до сих пор, о делении квадратного куска решетки любого размера вдоль ее линий на минимальное число меньших квадратов, см. гл. 15 книги М. Гарднера «Математические новеллы» (М., изд-во «Мир», 1974).

Насколько мне известно, соответствующая задача для треугольной решетки еще не рассматривалась. — М. Г. ]

337. На рисунке показано, как разрезать квадрат на 4 части одинакового размера и одной формы так, чтобы в каждой из частей содержалось по звездочке и по крестику,

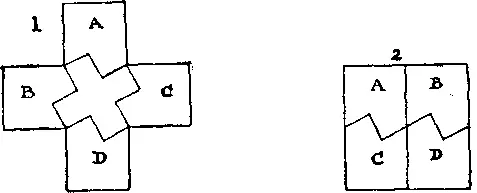
338. Если вырезать греческий крест меньших размеров (см. случай 1 ), то из четырех частей A , B , C и D можно сложить квадрат, показанный в случае 2 .

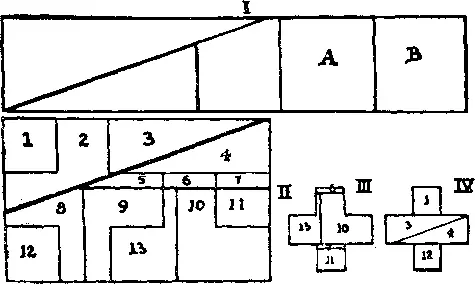
339. Отрежьте верхнюю и нижнюю части креста и поместите их в положения A и B (случай I ), а оставшуюся большую часть разрежьте на 3 части так, чтобы из полученных 5 частей сложить прямоугольник, изображенный в случае II . Можно сказать, что этот прямоугольник составлен из 15 квадратов — по 5 квадратов на каждый новый крест. Остальные разрезы провести нетрудно. Из частей 2, 5, 8, 9 с очевидностью получается один крест; из частей 13, 6, 10, 7 и 11 — второй (случай III ), а из 1, 3, 4, 12 получается третий крест (случай IV ). Площадь каждого конца малого креста составляет ⅓ площади любого конца большого креста.

(Число частей можно понизить до 12. — М. Г. ]

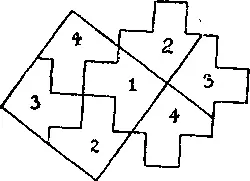
340. Как следует разрезать данную фигуру на 4 части, чтобы из них получился квадрат, показано на рисунке.

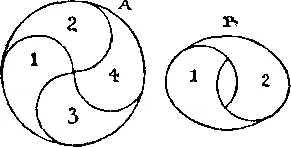
341. В случае A изображен круг, разделенный на 4 части, образующие «великую Монаду», а в случае B показано, как из двух таких частей можно составить один табурет (второй табурет получается аналогично из частей 3 и 4 ). Правда, отверстия для руки располагаются поперек, а не вдоль овалов, тем не менее все условия задачи выполнены.

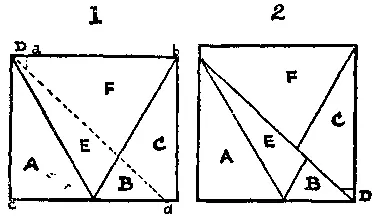
342. Разрежьте один из треугольников пополам и сложите части вместе, как показано в случае 1 . Затем проведите разрез вдоль пунктирных линий так, чтобы и ab , и cd равнялись стороне искомого квадрата. Затем сложите полученные части вместе, как показано в случае 2 , сдвинув F и C влево вверх и переместив маленький кусочек D из одного угла в другой.

[Существует решение данной задачи, содержащее только 5 частей. — М. Г. ]

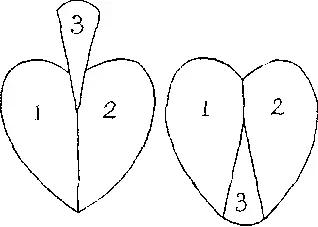
343. На рисунке показано, как можно разрезать символ масти пик на три части, чтобы получить символ червовой масти.

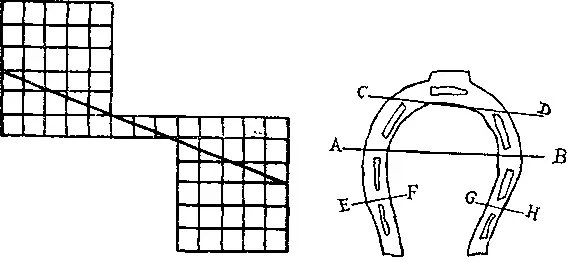
344. Вы видите на рисунке, как следует расположить 4 части, чтобы одна клетка исчезла (на первый взгляд). Объяснение этого феномена состоит в том, что края частей, расположенные вдоль жирной линии, не совпадают по направлению. Если вы расположите внешние края данной фигуры точно под прямым углом, то некоторые части перекроются и площадь перекрытой поверхности окажется равной площади одной клетки. Вот в чем и состоит простое объяснение нашего парадокса.

345. Прежде всего проведите разрез AB . Затем сложите полученные три части вместе так, чтобы при следующем взмахе ножниц вы могли провести одновременно разрезы CD , EF и GH (см. рисунок справа).

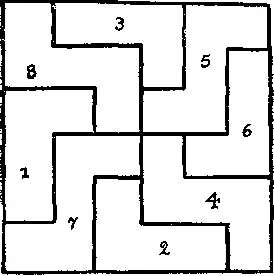
346. Восемь кусков фанеры можно расположить симметрично, чтобы они образовали квадрат таким образом, как показано на рисунке.

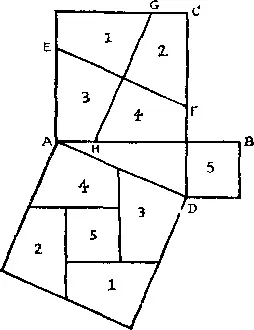
347. Сложите два квадрата вместе таким образом, чтобы линии AB и CD были прямыми. Затем найдите центр большего квадрата и проведите через него прямую EF , параллельную AD . Если вы теперь проведете через тот же центр перпендикулярно EF прямую GH , то больший квадрат разобьется на 4 части, из которых вместе с меньшим квадратом можно будет составить новый квадрат.

[Это решение было впервые найдено английским математиком-любителем Генри Перигейлом, который опубликовал его в 1873 г. Оно представляет собой одно из лучших доказательств теоремы Пифагора с помощью разрезания. См. гл. 38 книги М. Гарднера «Математические головоломки и развлечения» (М., изд-во «Мир», 1971). — М. Г. ].

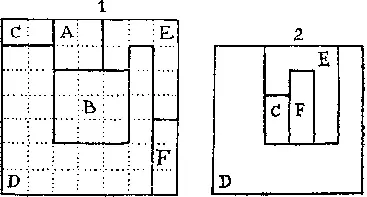
348. На рисунке показано, как можно разрезать фанеру. Квадраты A и B вырезаются целиком (1) , а из четырех частей C , D , E и F можно составить третий квадрат (2) .

[Существуют решения данной задачи, в которых участвует только пять частей. Не сможет ли читатель отыскать решение из пяти частей, при котором общая длина разрезов составляет 16 единиц? — М. Г. ]

349. Вырежьте кусок A и, повернув его на четверть оборота по часовой стрелке, соедините с куском B . При этом получится правильная шахматная доска.

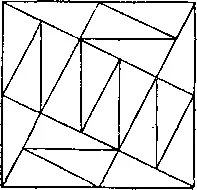
350. На рисунке показано, как составить квадрат из 20 кусочков.

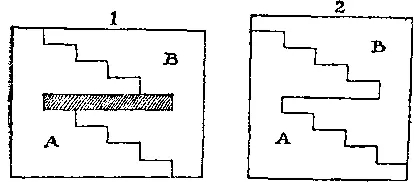
351. Если ковер разрезать на две части, как показано в случае 1 , и сшить куски вместе таким образом, как изображено в случае 2, то получится квадрат. Ширина ступеньки равна 2, а высота 1 м.