Генри Дьюдени - Пятьсот двадцать головоломок

На этот вопрос я получил тот же самый ответ (Пэт, очевидно, мог измерять все расстояния только от Пигтауна):

— Ровно вдвое меньше, чем отсюда до Пигтауна. Прошел еще час, и наше путешествие закончилось. Каково расстояние от Богули до Болифойна?

95. Задача о пешеходах.Один человек, гуляя за городом, оглянулся назад и заметил приятеля, который шел в том же направлении, но на 400 м сзади него. Глядя друг на друга, приятели прошли по прямой еще по 200 м каждый. Вам кажется, что они должны были встретиться? Ничуть не бывало, между ними после этого все еще оставалось расстояние 400 м.

Как это могло получиться?

96. Неверные весы.Когда пудинг положили на одну чашку весов, то они показали на 4 г больше, чем его истинного веса. Когда же его положили на другую чашку, то весы показали на 48 г больше, чем в первом случае. Каков истинный вес пудинга?

97. Обвес.Один лавочник, чьи моральные устои за годы войны весьма пошатнулись, дошел до того, что завел у себя в лавке неверные весы. (На рисунке можно заметить, что одно плечо их коромысла длиннее другого, хотя рисунок специально сделан так, чтобы не подсказать ответа.) При одном взвешивании на этих весах 3 банки уравновесили 8 пакетов (содержимое банок и пакетов для нас несущественно), а при другом — 1 пакет уравновесил 6 банок.

Известно, что истинный вес одной банки равен 1 кг, Сколько весят 8 пакетов?

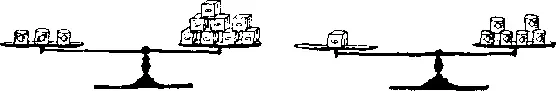
98. Взвешивание ребенка.

— Прошлым летом я был свидетелем одного забавного случая на железнодорожной станции, — сказал мой приятель. — Небольшая семья стояла перед автоматическими весами, рассчитанными на 200 фунтов, безрезультатно пытаясь решить трудную задачу — взвесить ребенка. Едва родители оставляли ребенка одного на весах, он начинал реветь и спрыгивал с них, при этом отцу приходилось удерживать собаку, тоже желавшую принять участие в этой операции. Наконец, отец вместе с ребенком и Фидо взобрался на весы, а я их сфотографировал.

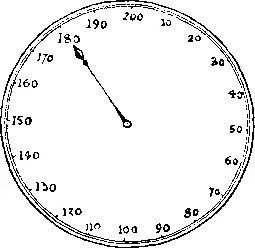
Тут приятель показал мне фотографию, с которой я срисовал только показание весов, поскольку остальное меня не интересовало (см. рисунок).

— После этого мужчина повернулся к своей жене и сказал: «Мне кажется, дорогая, что вместе с ребенком я вешу на 162 фунта больше, чем собака, а собака весит на 70% меньше, чем ребенок. Нам дома следует все хорошенько обдумать».

Мне тоже захотелось разобраться самому в этой задаче. Как вы думаете, сколько весило милое дитя?

99. Фрукты для варенья.Для варки варенья понадобилось взвесить свежие фрукты. Оказалось, что яблоки, груши и сливы уравновешивают друг друга, как показано на рисунке.

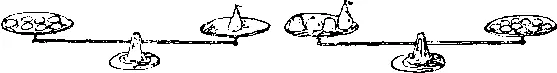
Не могли бы вы сказать, сколько слив уравновесят одну грушу? Относительные размеры плодов на рисунке изображены неверно (это сделано специально), но мы должны считать, что плоды одного вида равны по весу.

Очевидно, что 3 яблока и груша весят столько же, сколько 10 слив, и что яблоко и 6 слив уравновешивают одну грушу. Но вот сколько слив потребуется, чтобы уравновесить грушу?

100. Взвешивание чая.Бакалейщику потребовалось расфасовать 20 фунтов китайского чая по двухфунтовым пакетам, но у него куда-то запропастились гири. После тщетных поисков он нашел только пяти- и девятифунтовую гири.

Как может бакалейщик наиболее быстро выполнить свою работу? Скажем сразу, что произвести требуется лишь 9 взвешиваний.

101. Особое число.Какое число образовано из пяти последовательных цифр (идущих не обязательно по порядку) так, что число, образованное первыми двумя цифрами, умноженное на среднюю цифру, дает число, образованное последними двумя цифрами. (Например, если мы возьмем число 12 896, то 12, умноженное на 8, дает 96. Но, к несчастью, 1, 2, 6, 8, 9 не являются последовательными цифрами, так что этот пример в качестве решения не пригоден.)

102. Пять карточек.У меня пять карточек, на которых изображены цифры 1, 3, 5, 7 и 9. Как расположить их в ряд таким образом, чтобы произведение числа, образованного первой парой карточек, на число, образованное последней парой карточек, минус число, стоящее на средней карточке, равнялось числу, составленному из повторений одной и той же цифры? Например (см. рисунок), 31, умноженное на 79, минус 5 равно 2444; последнее число подошло бы нам, если бы вместо 2 на первом месте стояло тоже число 4.

Очевидно, должно быть два решения, поскольку обе пары карточек — две первые и две последние — расположены совершенно симметрично.

103. Цифры и квадраты.Какой наименьший квадрат целого числа оканчивается наиболее длинной последовательностью одинаковых цифр?

Так, если бы наиболее длинная последовательность одинаковых цифр составила пять, то нам подошло бы число 24 677 777 (разумеется, если бы оно было наименьшим квадратом, но это неверно). Нуль не считается допустимой цифрой.

104. Две суммы.Можете ли вы расположить цифры 1, 2, 3, 4, 5, 7, 8, 9 двумя группами по четыре цифры в каждой так, чтобы суммы чисел, составленных из цифр каждой группы, были равны между собой?

Очень просто получить ответ, заменив 9 на 6. Например, каждая из сумм двух групп чисел 1, 2, 7, 8 и 3, 4, 5, 6 равна 18. Но такая замена не допускается.

105. Повторяющаяся четверка цифр.Если мы умножим 64 253 на 365, то получим 23 452 345, где первые четыре цифры повторяются.

На какое наибольшее число нужно умножить 365, чтобы получить аналогичное произведение, содержащее восемь цифр, из которых первые четыре повторяются?

106. Легкое деление.Разделив число 8 101 265 822 784 на 8, вы убедитесь, что ответ можно получить, просто переставив 8 из начала в конец числа!

Не могли бы вы найти число, начинающееся с 7, которое можно разделить на 7 столь же простым способом?

107. Недоразумение.Один американский читатель попросил меня найти число, составленное из любого количества цифр, для которого деление на 2 можно выполнить, переставив последнюю цифру в начало. По-видимому, эта задача возникла у него после того, как он познакомился с неправильно сформулированной предыдущей задачей. Если бы требовалось переставить в конец первую цифру, то ответом служило бы число 315 789 473 684 210 526, а отсюда легко было бы найти решение, начинающееся с любой цифры. Но если требуется переставить цифру из конца в начало, то для делителя 2 решения нет. Однако существует решение для делителя 3. Не могли бы вы его найти?