Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

1.1.Вокруг правильного треугольника ABC описана окружность O радиусом R . Окружность O 1касается двух сторон AB и BC треугольника и окружности O . Найдите расстояние от центра окружности О 1до вершины А .

1.2.Высота равнобедренного треугольника с углом α при основании больше радиуса вписанного в него круга на m . Определите основание треугольника и радиус описанной окружности.

1.3.Докажите, что радиус окружности, делящей пополам стороны треугольника, вдвое меньше радиуса окружности, описанной около этого треугольника.

1.4.В треугольнике соединены основания биссектрис. Найдите отношение площади данного треугольника к площади образовавшегося треугольника, если стороны данного треугольника относятся как p : q : l .

1.5.Даны углы A, B, C треугольника ABC . Пусть окружность касается сторон BC , AC и AB треугольника соответственно в точках A 1, B 1, C 1. Найдите отношение площади треугольника A 1 B 1 C 1к площади треугольника ABC .

1.6.Дан треугольник ABC , углы B и C которого относятся как 3 : 1, а биссектриса угла А делит площадь треугольника в отношении 2 : 1. Найдите углы треугольника.

1.7.Найдите длину l биссектрисы внешнего угла А треугольника, если даны его стороны b и c и угол А между ними ( b ≠ c ).

1.8.В треугольнике площади S , с острым углом α при вершине А биссектриса угла А в p раз меньше радиуса описанного и в q раз больше радиуса вписанного круга. Найдите сторону треугольника, лежащую против угла А .

1.9.В треугольнике ABC проведены биссектрисы AM и BN. Пусть O — точка их пересечения. Известно, что

AO : OM = √3 : 1, а BO : ON = 1 : (√3 − 1).

Найдите углы треугольника.

1.10.Внутри угла а взята точка M . Ее проекции P и Q на стороны угла удалены от вершины O угла на расстояния OP = p и OQ = q . Найдите расстояния MP и MQ от точки M до сторон угла.

1.11.В остроугольном треугольнике две высоты равны 3 и 2√2 см, а их точка пересечения делит третью высоту в отношении 5 : 1, считая от вершины треугольника. Найдите площадь треугольника.

1.12.В треугольнике ABC разность углов B и C равна π/ 2. Определите угол C , если известно, что сумма сторон b и c равна k , а высота, опущенная из вершины A , равна h .

1.13.В треугольнике ABC имеется точка O , такая, что углы ABO , ВСО и CAO равны α. Выразите ctg α через площадь треугольника и его стороны.

1.14.В треугольнике ABC дана разность φ углов A и В (φ = A − В > 0). Известно, что высота, опущенная из С на AB, равна BC − AC . Найдите углы треугольника.

1.15.Даны длины высот AA 1= h a и ВВ 1= h b треугольника ABC и длина CD = l биссектрисы угла С . Найдите угол С .

1.16.В треугольник с основанием а и противоположным углом α вписана окружность Через центр этой окружности и концы основания треугольника проведена вторая окружность Найдите ее радиус.

1.17.Докажите, что если длины сторон треугольника образуют арифметическую прогрессию, то центр окружности, вписанной в этот треугольник, и точка пересечения его медиан лежат на прямой, параллельной средней по длине стороне треугольника.

1.18.В треугольнике ABC радиус вписанной окружности равен r , сторона BC больше r в k раз, а высота, опущенная на эту сторону, больше r в 4 раза. Найдите полупериметр p , tg A / 2и стороны b и c .

1.19.Углы С, A, В треугольника ABC образуют геометрическую прогрессию со знаменателем 2. Пусть O — центр окружности, вписанной в треугольник ABC , K — центр вневписанной окружности, касающейся стороны AC , L — центр вневписанной окружности, касающейся стороны BC . Докажите, что треугольники ABC и OKL подобны.

1.20.В треугольнике ABC углы A , В и С образуют геометрическую прогрессию со знаменателем 2. Докажите, что

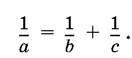
1.21.Докажите, что если P , Q , R — соответственно точки пересечения каждой из сторон BC , CA , AB (или их продолжений) треугольника ABC с некоторой прямой, то

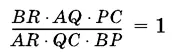
(теорема Менелая) .

1.22.Точка D находится на стороне BC треугольника ABC. Докажите, что

AB ² · DC + AC ² · BD − AD ² · BC = BC · DC · BD

(теорема Стюарта) .

1.23.На сторонах треугольника ABC взяты точки P , Q и R так, что три прямые AP , BQ и CR пересекаются в одной точке. Докажите, что

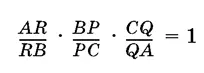
(теорема Чевы) .

1.24.Через произвольную точку O , взятую внутри треугольника ABC , проведены прямые DE , FK , MN , параллельные соответственно AB , AC , BC , причем F и M лежат на AB , E и K — на BC , N и D — на AC . Докажите, что

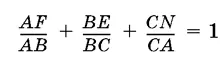
1.25.Через центр O правильного треугольника ABC проведена произвольная прямая. Докажите, что сумма квадратов расстояний от вершин треугольника до этой прямой не зависит от выбора прямой.

1.26.Вокруг треугольника ABC , в котором а = 2, b = 3 и угол C = 60°, описана окружность. Определите радиусы окружностей, проходящих через две вершины треугольника и центр описанной окружности.

1.27.Стороны треугольника связаны соотношением а ² = c ( b + с ). Докажите, что угол A вдвое больше угла C .

1.28.Пусть O — центр окружности, вписанной в треугольник ABC . Докажите, что если OA ² = OB · OC , то

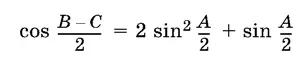
1.29.Площадь , треугольника ABC удовлетворяет соотношению S = а ² − ( b − с )². Найдите угол A .

1.30.На сторонах треугольника внешним образом построены квадраты. Докажите, что расстояние между центрами квадратов, построенных на боковых сторонах, равно расстоянию от центра квадрата, построенного на основании, до противоположной вершины треугольника.