Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
4.Банк планирует вложить на один год 40% имеющихся y него средств клиентов в проект X , а остальные 60% — в проект Y . В зависимости от обстоятельств проект X может принести прибыль в размере от 19 до 24% годовых, а проект Y — от 29 до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определите наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты X и Y .
5.Функция f ( x ) определена на всей числовой прямой, является нечетной, периодической с периодом 4, и на промежутке 0 ≤ x ≤ 2 ее значения вычисляются по правилу f ( x ) = 1 − | x − 1|. Решите уравнение
2 f ( x ) f ( x − 8) + 5 f ( x + 12) + 2 = 0.
6.Найдите все значения параметра а , при которых периметр фигуры, заданной на координатной плоскости условием
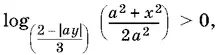
будет наименьшим.
Московский государственный университет экономики, статистики и информатики (МЭСИ)
1.Найдите положительный тангенс угла между касательными к гиперболе xy = 1 в точках с абсциссами х 1= 1, х 2= 2.
2.Найдите (в радианах) все решения уравнения
tg³ x ² + tg² x ² + ctg² x ² + ctg³ x ² − 4 = 0.
3.Найдите наименьшее значение выражения
x ² + y ² + 2/ | x |·| y |.
4.Вычислите, если x < 0:
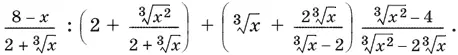
5.Вектор 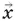 , коллинеарный вектору {12; −16; −15}, образует острый угол с осью Oz . Зная, что
, коллинеарный вектору {12; −16; −15}, образует острый угол с осью Oz . Зная, что 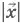 = 100, найдите его первую координату.
= 100, найдите его первую координату.
6.Решите уравнение
log 1 + 2 x (6 x ² + 5 x + 1) − log 1 + 3 x (4 x ² + 4 x + 1) = 2.
7.Найдите наибольшее целое решение неравенства
9 · 16 −1/ x + 5 · 36 −1/ x < 4 · 81 −1/ x .
8.Производительность труда рабочего повышалась дважды на одно и то же число процентов. На сколько процентов возрастала каждый раз производительность труда, если за одно и то же время рабочий раньше вырабатывал изделий на 25 000 р., а теперь — на 28 000 р.?
9.Найдите квадрат биссектрисы внутреннего угла С треугольника АВС , если АВ = 2, ВС = 4, АС = 2.
10.Ребро куба равно 36. Найдите кратчайшее расстояние между диагональю куба и скрещивающейся с ней диагональю основания куба.
Примечания
1
Эту задачу нужно решать с особым вниманием.
2
Ответы к упражнениям 1—22 см. на с. 326—328.
3
Для краткости равенства можно располагать в строку или писать ( x , y , z , ...) = ( а , b , с , ...).
4
Имеется в виду применение абсолютного тождества, см. с. 42. Для неабсолютных тождеств это утверждение неверно.
5
Под применением тождества мы понимаем замену его левой части на правую.
6
Два совпадающих решения считаются за одно.
7
Ответы к упражнениям 1—9 см. на с. 360.
8
Если какая-то точка уже была отмечена светлым кружком, то изменять обозначение не следует.
9
Так в источнике (прим. от верстальщика fb2).
10
Требуется найти не только положительные значения x .
11
Требуется найти не только положительные значения x .
12
1 карат = 0,2 г.
13
Плотности всех растворов предполагаются одинаковыми; при сливании двух растворов объем нового раствора равен сумме объемов исходных растворов.
14
Первое соотношение — неабсолютное тождество, остальные — абсолютные тождества.
15
Так в тексте. От верстальщика fb2.
16
[ x ] — целая часть числа x .
17
Такое преобразование системы, вообще говоря, может привести к приобретению постороннего решения, в котором y = 0.
20
Хотя метод интервалов был изложен во введении применительно к многочленам, им можно пользоваться при решении более широкого класса неравенств. В частности, для этого неравенства получаем
(3 √ x − 2)( x + 1)( x − 3/ 2) >0.
Первый множитель обращается в нуль при 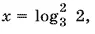 причем он больше нуля при
причем он больше нуля при 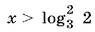 и меньше нуля при
и меньше нуля при 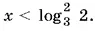 Нанесем точки −1,
Нанесем точки −1, 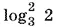 и 3/ 2на числовую ось и воспользуемся тем обстоятельством, что при x > 3/ 2все три скобки положительны. Так как, кроме того, x ≥ 0, окончательно получим
и 3/ 2на числовую ось и воспользуемся тем обстоятельством, что при x > 3/ 2все три скобки положительны. Так как, кроме того, x ≥ 0, окончательно получим
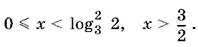
21
Заметим, что если бы мы перешли к основанию 2, то получили бы уравнение, равносильное данному. Убедитесь в этом самостоятельно.
22
Формулы для 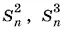 и т. п. доказываются аналогично с помощью тождеств: ( x + 1)³ = x ³ + 3 x ² + 3 x + 1, ( x + 1) 4= x 4+ 4 x ³ + 6 x ² + 4 x + 1.
и т. п. доказываются аналогично с помощью тождеств: ( x + 1)³ = x ³ + 3 x ² + 3 x + 1, ( x + 1) 4= x 4+ 4 x ³ + 6 x ² + 4 x + 1.
23
Во всех случаях удобно граничную точку относить к обоим интервалам, чтобы не столкнуться с ситуацией, когда наименьшее значение не достигается.
Интервал:
Закладка:










