Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Ответ. 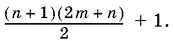
Глава 22
Обратные тригонометрические функции
22.1.Введем обозначения:

В этих обозначениях равенство примет вид
2α = π/ 4− β,
причем правая и левая части лежат в интервале (0, π/ 2). Возьмем тангенсы от каждой из частей:

Так как тангенс является монотонной функцией в интервале (0, π/ 2), то равенство доказано.
22.2.Пусть
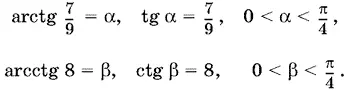
Так как 0 < α + β < π/ 2и

Наше выражение принимает теперь вид
π/ 4+ arcsin √2/ 4.
Поскольку arcsin √2/ 4> arcsin √2/ 2, то
0 < π/ 4+ γ < π/ 2,
где γ = arcsin √2/ 4и sin γ = √2/ 4. Найдем

Поскольку мы оказались в интервале монотонности синуса, то остается воспользоваться определением арксинуса.
Ответ.arcsin [ √7 + 1/ 4].
22.3.Рассмотрим сначала первое и третье слагаемые:
arctg (−2) = α, tg α = −2, − π/ 2< α < 0;
arctg (−⅓) = β, tg β = −⅓, − π/ 2< β < 0.
Таким образом, −π < α + β < 0, что не является областью главных значений какой−нибудь обратной тригонометрической функции. Поэтому прибавим ко всем частям неравенства π: 0 < π + α + β < π. Теперь π + α + β попадет в область значений арккотангенса, что обеспечивает взаимно однозначный переход к обратным функциям. Найдем

Следовательно,
π + α + β = arcctg (− 1/ 7), т. е. α + β = −arcctg 1/ 7.
Наше выражение равно arcsin ⅓ − arcctg 1/ 7. Пусть
arcsin ⅓ = γ, sin γ = ⅓, 0 < γ < π/ 2;
arcctg 1/ 7= δ, ctg δ = 1/ 7, 0 < δ < π/ 2.
Так как − π/ 2< γ − δ < π/ 2, что является интервалом значений арксинуса, то вычислим синус от γ − δ:
sin (γ − δ) = sin γ cos δ − cos γ sin δ.
Так как
cos γ = 2√2/ 3, cos δ = 1/ 5√2, sin δ = 7/ 5√2,
то

Ответ.arcsin √2 − 28/ 30.
22.4.Сумма существует при 0 ≤ x ≤ 1. Введем обозначения и используем определение арксинуса:
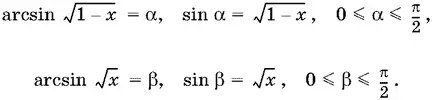
Так как сумма α + β лежит в интервале [0, π], который является интервалом монотонности косинуса, то имеется взаимно однозначное соответствие между α + β и cos (α + β) при условии, что 0 ≤ x ≤ 1. Так как

то α + β = π/ 2.
Ответ. π/ 2при 0 ≤ x ≤ 1.
22.5.Оценим φ = π( x ² + x − 3), если 0 ≤ x ≤ √3 − 1/ 2.
Имеем

Следовательно,
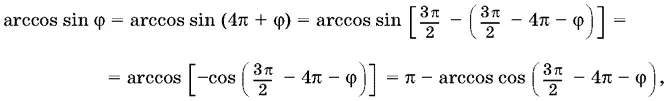
где 0 ≤ 3π/ 2− 4π − φ ≤ π/ 2. Окончательно получаем
arccos sin φ = π − 3π/ 2+ 4π + φ = 7π/ 2+ φ.
Ответ. 7π/ 2+ π( x ² + x − 3).
22.6.При 0 ≤ x ≤ 1 оба арксинуса существуют. Для первого это очевидно, а для второго имеем
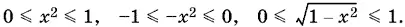
Следовательно,
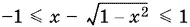
и, тем более,

Введем обозначение
arcsin x = α, sin α = x , 0 ≤ α ≤ π/ 2;

Нужно доказать, что α − β = π/ 4, или α − π/ 4= β. Так как − π/ 4 ≤ α − π/ 4≤ π/ 4, то α − π/ 4и β лежат в интервале монотонности синуса. Поэтому, если мы докажем, что синусы этих аргументов равны, то тем самым будет доказано и равенство самих аргументов. Поскольку
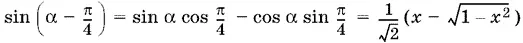
(перед корнем взят знак плюс, так как cos α ≥ 0 при 0 ≤ α ≤ π/ 2).
Итак, доказано, что sin (α − π/ 4) = sin β, откуда следует справедливость нашего равенства.
22.7.Так как x < −1, то −1 < 2 x / 1 + x ²< 0. Введем обозначения
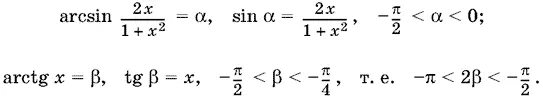
Следовательно,
− 3π/ 2 < α + 2β < − π/ 2,
т. е. данное выражение лежит в интервале монотонности синуса. Найдем

После подстановки получим

т. е. α + 2β = −π.
Ответ.−π.
22.8.Из уравнения следует, что
arcsin x = π/ 12+ n π/ 3.
Поскольку − π/ 2≤ arcsin x ≤ π/ 2, то возможны лишь три значения n = 0, −1, 1.
Если n = 0, то arcsin x = π/ 12,
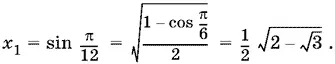
Если n = −1, то arcsin x = − π/ 4,
x 2= sin (− π/ 4) = − 1/ √2.
Если n = 1, то arcsin x = 5π/ 12,
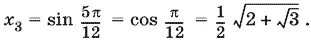
Ответ. 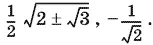
22.9.Если x — корень данного уравнения, то и − x будет его корнем. Поэтому достаточно найти лишь неотрицательные корни. Если x ≥ 0, то
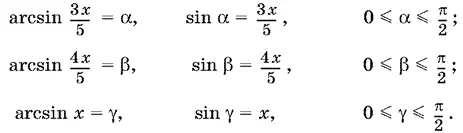
Перенеся α в правую часть уравнения, получим β = γ − α, причем 0 ≤ β ≤ π/ 2и − π/ 2 ≤ γ − α ≤ π/ 2. Поскольку обе части уравнения находятся в интервале монотонности синуса, то данное уравнение равносильно такому:
sin β = sin (γ − α).
Последнее уравнение можно записать в виде
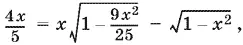
добавив к нему условие | 4 x / 5| ≤ 1, являющееся в данном случае следствием уравнения. Получаем x 1= 0.
Остается 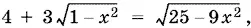 а после возведения в квадрат
а после возведения в квадрат 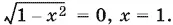
Интервал:
Закладка:










