Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Остается исследовать

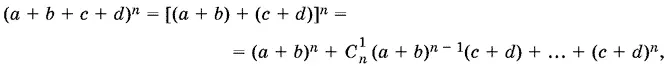
Так как условие n ≥ 2, из которого следует, что m ≥ 2, должно выполняться и для k 2, то формула (3) по сравнению с (2) может дать лишь одно дополнительное значение: m = 2. Однако при m = 2 получим, что k 2= 2 и n = 2. Это противоречит требованию k ≤ n − 1. Таким образом, формула (3) не дает новых значений m , а следовательно, и n .

Ответ. n = m ² − 2, где m = 3, 4, 5, ... .

21.9.Так как

( a + b + c + d ) n = [( a + b ) + ( c + d )] n = ( a + b ) n + C n 1( a + b ) n − 1( c + d ) + ... + ( c + d ) n ,

то после раскрытия скобок получим все неподобные члены. Их число будет равно

( n + 1) · 1 + n · 2 + ( n − 1) · 3 + ... + 2 n + 1( n + 1),

где для симметрии к крайним членам приписаны множителями единицы. Чтобы вычислить эту сумму, запишем ее k −й член: ( n + 2 − k ) = ( n + 2) k − k ². Тогда наша сумма примет вид

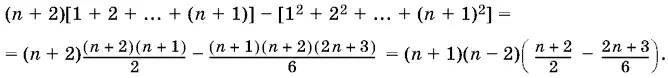
Ответ.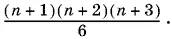

21.10.Предположим, что 0 ≤ k ≤ n − 1. Запишем данное выражение в виде

(1 + x + x ² + ... + x k − 1+ x k + x k + 1+ ... + x n − 1)².

Члены, содержащие x k , могут быть получены только в результате почленного перемножения членов суммы 1 + x + x ² + ... + x k − 1+ x k с членами той же суммы, записанной в обратном порядке, т. е.

1 · х k , x · х k − 1, ..., х k − 1 · x , x k · 1

Так как слагаемых будет k + 1, то и коэффициент при x k будет равен k + 1.

Предположим теперь, что n − 1 < k ≤ 2( n − 1). Тогда нужно почленно перемножить суммы

x k − n + 1+ ... + x n − 1, x n − 1+ ... + x k − n + 1,

в результате чего получим 2 n − k − 1 членов, содержащих x k .

Ответ. k + 1, если 0 ≤ k ≤ n − 1;

2 n − k − 1, если n − 1 < k ≤ 2 n − 2.

21.11.Сравним коэффициент члена разложения с номером k + 1 с коэффициентом десятого члена разложения:

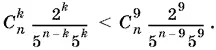
Так как знаменатели одинаковы, то

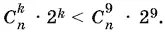
Поскольку десятый член разложения имеет наибольший коэффициент, то он больше девятого и больше одиннадцатого:

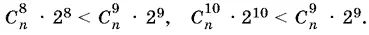
Из первого неравенства следует, что

Из второго

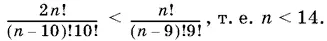
Ответ. n = 13.

21.12.Преобразуем выражение, стоящее в левой части, следующим образом:

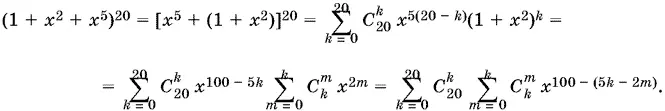
Вопрос состоит в следующем: если k , m = 1, 2, ..., 20, причем m ≤ k , то какие значения от 0 до 100 принимает выражение 5 k − 2 m .

Если m = 0, 1, 2, 3, 4, то получим соответственно 5 k , 5 k − 2, 5 k − 4, 5 k − 6, 5 k − 8. Если бы k не было связано ограничениями, то мы получили бы все числа, так как в эти пять выражений вошли числа, дающие при делении на 5 в остатке 0, 3, 1, 4 и 2 соответственно. Однако k = 0, 1, ..., 20 и, кроме того, k ≥ m . Так как 5 k получено при m = 0, то k может принимать все свои 21 значение, в результате чего получим все числа, кратные 5 от 0 до 100. Рассмотрим теперь числа, которые при делении на 5 дают в остатке 1. У нас они записаны в виде 5 k − 4 и получились при m = 2, в силу чего k = 2, 3, ..., 20. В результате мы получим 19 чисел, дающих при делении на 5 в остатке 1. В эту группу не войдет лишь число 1. Числа, дающие в остатке 2, записаны в виде 5 k − 8, где k ≥ 4. Следовательно, 5 k − 8 = 12, 17, ..., 92, т. е. выпадают числа 2, 7 и 97. Для чисел вида 5 k − 2 переменная k = 1, 2, ..., 20 и 5 k − 2 = 3, 8, ..., 98, куда вошли все числа, дающие в остатке 3. Среди чисел вида 5 k − 6, где k = 3, ..., 20, мы не встретим 4 и 99.

Числа 1, 2, 4, 7, 97 и 99 не могут быть получены из выражения 5 k − 2 m и при m > 4. В самом деле, с одной стороны, 5 k − 2 m ≥ 5 m − 2 m = 3 m > 12, а с другой стороны,

5 k − 2 m < 5 k − 8 ≤ 100 − 8 = 92,

т. е.

12 < 5 k − 2 m < 92.

Итак, выпали 6 чисел 1, 2, 4, 7, 97 и 99, т. е. будут отсутствовать члены с показателями 99, 98, 96, 93, 3, 1.

Ответ.95.

21.13.Пусть Р n — ответ на вопрос задачи для последовательности, состоящей из n элементов. В первой группе может оказаться либо один элемент ( а 1), либо два элемента ( а 1, а 2). Разбиений, содержащих в первой группе один элемент ( а 1), будет столько, сколько разбиений можно образовать из n − 1 оставшихся членов последовательности а 2, а 3, ..., а n , т. е. Р n − 1. Разбиений же, содержащих в первой группе два элемента, будет Р n − 2, так как после образования группы ( а 1, а 2) останется n − 2 элементов а 3, ..., а n .

Итак

Р n = Р n − 1+ Р n − 2.

Такая формула называется рекуррентной, потому что, зная Р 1и Р 2и применяя ее последовательно, мы получим Р 3, затем Р 4и т. д. Поскольку Р 1= 1, а Р 2= 2, то Р 3= 3, Р 4= 5, Р 5= 8, Р 6= 13, Р 7= 21, Р 8= 34, Р 9= 55, Р 10= 89.

Ответ.89.

21.14.Пусть на плоскости проведены m параллельных прямых. Они разобьют ее на m + 1 областей. Если провести еще одну непараллельную прямую, то областей станет 2( m + 1). Предположим, что k непараллельных прямых образуют, пересекаясь с m параллельными прямыми, М k областей. Если добавить еще одну прямую, пересекающую все имеющиеся, но не проходящую ни через одну из старых точек пересечения, то на этой прямой будет m + k точек пересечения с остальными прямыми, в результате чего образуется m + k + 1 новых областей.

Таким образом,

М k + 1= М k + m + k + 1.

Так как М о= m + 1, то

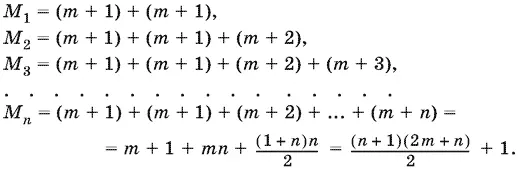
Остается доказать эту формулу методом математической индукции, что сводится к элементарным выкладкам, которые мы оставляем читателю.