Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

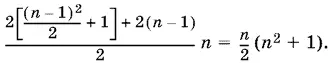
Ответы можно объединить.

Ответ. n / 2[ n ² + 3/ 2+ (−1) n ½].

20.11.Домножим S n на 2 sin π/ 2 n :

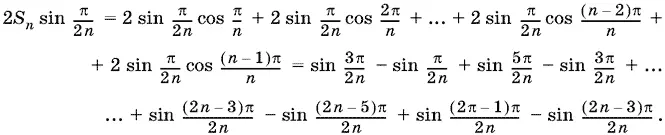
После приведения подобных получим

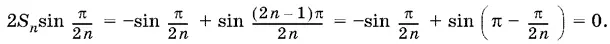
Так как sin π/ 2 n ≠ 0 при натуральных n , то S n = 0.

2 n

Ответ.0.

20.12.Обозначим искомую сумму через S . Тогда

2 S = 1 · 2 + 2 · 2² + 3 · 2³ + ... + 100 · 2 100,

2 S − S = 100 · 2 100− (1 + 2 + 2² + ... + 2 99) = 100 · 2 100− (2 100− 1) = 99 · 2 100+ 1.

20.13.Пусть искомая сумма равна S. Разделим каждый член данного ряда на 2:

¼ + 3/ 8+ 5/ 16+ 7/ 32+ ... = S / 2

и вычтем полученный ряд из данного. Получим ряд:

½ + ½ + ¼ + 1/ 8+ 1/ 16+ ...,

сумма которого равна 3/ 2. Однако, с другой стороны, его сумма есть ни что иное, как S − S / 2 = S / 2. Таким образом, S / 2= 3/ 2 и, следовательно, S = 3.

Ответ.3.

21.1.Присвоим каждому из сидящих за круглым столом номер: а 1, а 2, ..., а n . Образовывая циклические перестановки: а n , а 1, а 2, ..., а n − 1; а п − 1, а n , а 1, а 2, ..., а п − 2и т. д., мы будем получать тот же способ размещения за столом. Таких циклических перестановок можно составить n .

Кроме этого, нужно учесть, что сосед слева и сосед справа неразличимы, т. е. перестановки а 1, а 2, ..., а п и а 1, а n , а n − 1, ..., а 2дают одно и то же размещение за столом. Так как всего возможно n ! перестановок, из которых каждые 2 n одинаковы, то искомое число равно

n !/ 2 n = ½( n − 1)!.

Ответ.½( n − 1)!.

21.2.Всего из пяти элементов можно составить Р 5перестановок. Среди них будет Р 4, y которых на первом месте а 1, и Р 4, y которых на первом месте а 2. Однако перестановки, y которых на первом месте а 1, а на втором месте а 2, попали и в первую, и во вторую группы. Таких перестановок Р 3.

Поэтому искомое число перестановок равно

Р 5− (2 P 4− Р 3) = 78.

Ответ.78.

21.3.Из семи разрядов три должны быть заняты двойками, что дает 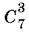вариантов. На каждое из оставшихся мест можно поместить любую из восьми цифр, благодаря чему каждый из предыдущих вариантов даст еще 8 4возможностей.

Ответ.

21.4.Предположим, что в каждое число входят три различные единицы: l 1, l 2, l 3, а остальные цифры 0, 2, 3, 4 и 5 равноправны. Тогда можно получить Р 8различных чисел. Отсюда нужно исключить Р 7чисел, начинающихся с нуля.

На самом деле разные единицы неразличимы. Другими словами, вместо одного числа мы получим Р 3одинаковых чисел, отличающихся лишь взаимными перестановками единиц.

Ответ.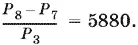

21.5.Предположим, что каюты неравноценны. Это дает в 8! раз больше вариантов, чем в случае равноценных кают, что мы учтем позднее.

В первую каюту можно заселить любых четырех из 32 экскурсантов, что можно сделать 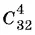способами, во вторую — любых четырех из 28 оставшихся и т. д. В итоге получим

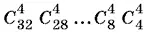
способов. Это число остается разделить на 8! и произвести упрощения.

Ответ. .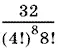

21.6.Рассмотрим k −й член суммы

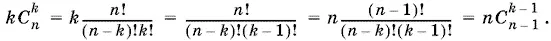
Данную сумму можно переписать в виде

Ответ. n · 2 n − 1.

21.7.Из разложения

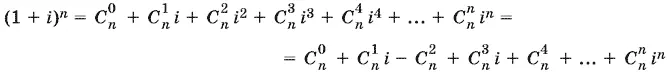
выделим действительную часть и приравняем действительной части комплексного числа (1 + i ) n . В самом деле,

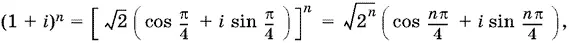
т. е.

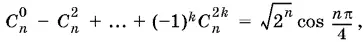
где n − 1 ≤ 2 k ≤ n .

Последнее ограничение означает, что через 2 k обозначено то из чисел n − 1 и n , которое является четным.

Ответ.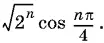

21.8.Условию задачи удовлетворяют такие n , для которых равенство

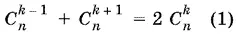
выполняется хотя бы для одного k . Заметим, что 1 ≤ k ≤ n − 1; n ≥ 2. Равенство (1) перепишем в виде

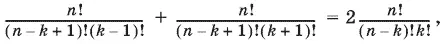
что после простых преобразований даст

4 k ² − 4 nk + п ² − n − 2 = 0,

откуда

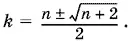
Чтобы выражение в правой части было целым, нужно сначала потребовать

n + 2 = m ², т. е. n = m ² − 2.

Поскольку n ≥ 2, то т ² ≥ 4 и m ≥ 2. Тогда

Если взять знак минус, получим

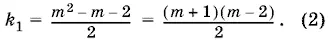
Число, стоящее в числителе, четное при всех m . Значение m = 2 нужно исключить, так как тогда k 1= 0, что невозможно. Если же m ≥ 3, то m + 1 ≥ 4, а m − 2 ≥ 1. Следовательно, k 1 ≥ 2. Потребуем теперь, чтобы выполнялось второе условие: k 1 ≤ n − 1, т. е. 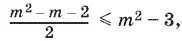что равносильно неравенству m ² + m − 4 ≥ 0. Последнее неравенство справедливо при всех m ≥ 3.