Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Кроме того, a рa r = a q ², a qa s = a r ², a pa s = a qa r , что отражает условие, в силу которого a р , a q , a r и a s образуют геометрическую прогрессию. Из первой группы формул имеем

Составим произведение ( p − q )( r − s ) и воспользуемся второй группой формул:

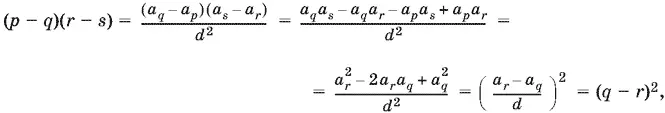
что и доказывает сформулированное в условии утверждение.

19.3.По условию

a = a 1+ d ( m − 1) = u 1 q m − 1, b = a 1+ d ( n − 1) = u 1 q n − 1, c = a 1+ d ( p − 1) = u 1 q p − 1.

Составим разности:

b − с = d ( n − p ), с − а = d ( p − m ), а − b = d ( m − n ).

Подставим в левую часть равенства, которое нужно доказать:

После несложных преобразований получим в обоих показателях нули, что и доказывает равенство произведения единице.

19.4.Перейдем в левой части равенства к общему основанию x и сделаем некоторые упрощения:

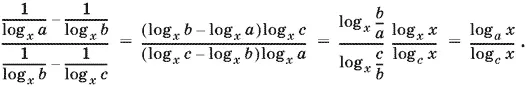
В последнем равенстве мы воспользовались тем, что b / a = c / b = q — знаменателю прогрессии, а также тем, что

19.5.Имеем

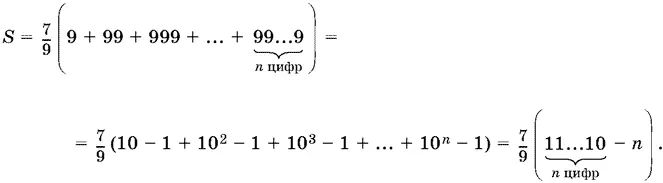
Ответ.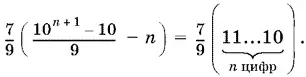

19.6.Преобразуем выражение, стоящее под знаком квадратного корня:

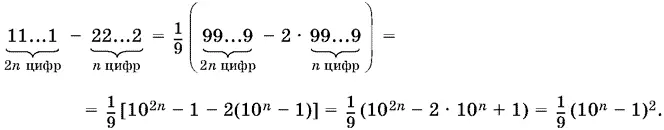
После извлечения квадратного корня получим

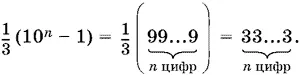
19.7.Из условия следует, что

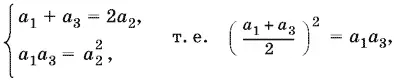
а следовательно, ( а 1− a 3)² = 0, а 1= а 3. Поскольку 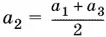, то а 2= а 1. Таким образом, а 1= а 2= а 3. Решим теперь систему уравнений

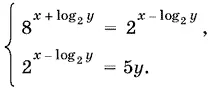
Первое уравнение можно последовательно преобразовать:

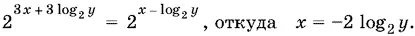
Подставив найденное значение x во второе уравнение системы, получим

Теперь можно найти x :

x = −2 log 2 y = ½ log 25.

Ответ.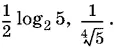

19.8.Пусть q — знаменатель прогрессии. Тогда по теореме Виета

x 1(1 + q ) = 3, x 1 q ²(1 + q ) = 12, x 1² q = A , x 1² q 5= B .

Из первых двух уравнений (подстановкой первого во второе) находим q ² = 4.

Так как последовательность по условию является возрастающей, то q = 2, откуда x 1= 1, что не противоречит тому, что прогрессия возрастающая.

Из двух вторых уравнений определяем А и В .

Ответ. А = 2, В = 32.

19.9.Пусть x 2= x 1 q , x 3= x 1 q ². Тогда по теореме Виета, примененной к данному уравнению, имеем

x 1+ x 1 q + x 1 q ² = 7, x 1² q + x 1² q ² + x 1² q ³ = 14.

Из первого уравнения получим x 1(1 + q + q ²) = 7. Это позволяет следующим образом преобразовать левую часть второго уравнения:

x 1² q (1 + q + q ²) = 7 x 1 q ,

откуда x 1= 2/ q . Подставим выражение для x 1в первое уравнение, получим

2(1 + q + q ²)/ q = 7, т. е. 2 q ² − 5 q + 2 = 0,

откуда

q 1= ½, q 2= 2.

Теперь для каждого из этих двух значений q можно найти x 1. При q = 1 получим, что x 1= 4, т. е. прогрессия убывающая. Во втором случае при q = 2 имеем x 1= 1, и прогрессия — возрастающая.

Ответ.1, 2, 4.

19.10.Из условия следует, что

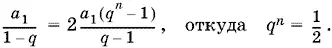
Произведение n первых членов прогрессии равно

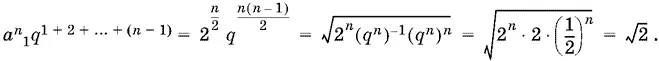
Ответ.√2.

19.11.Пусть а — цифра сотен, d — разность прогрессии. Искомое число делится на пять, если его последняя цифра либо 0, либо 5, т. е. либо а + 2 d = 0, либо а + 2 d = 5. Чтобы число делилось на девять, сумма его цифр должна делиться на девять. Но поскольку сумма трех цифр может изменяться от нуля до двадцати семи, имеются три возможности:

а + ( а + d ) + ( а + 2 d ) = 9; 18; 27.

Последнюю возможность отбрасываем, так как число 999 не делится на пять.

Пусть а + 2 d = 0. Если а + d = 3, то d = −3, а = 6. Получим число 630. Если а + d = 6, то d = −6, а = 12, что невозможно.

Пусть теперь а + 2 d = 5. Когда а + d = 3, получим d = 2, а = 1, что даст число 135. Когда а + d = 6, получим d = −1, а = 7, что приводит к числу 765. Поскольку все возможности исчерпаны, задача решена.

Ответ.630; 135; 765.

19.12.Задачу можно решить, обозначив через x цифру единиц, а через q знаменатель прогрессии. Используя условия задачи, мы придем к двум уравнениям:

100 xq ² + 10 xq + x − 594 = 100 x + 10 xq + xq ², ( x + 1) + ( xq ² + 1) = 2( xq + 2).

Первое уравнение можно переписать в виде

x ( q ² − 1) = 6,

а второе — в виде

x ( q ² − 2 q + 1) = 2, т. е. x ( q − 1)² = 2.

Деля первое уравнение на второе, получим

q + 1/ q − 1= 3, q = 2.

Следовательно, x = 2.

Задачу можно решить перебором, если воспользоваться тем, что цифры числа образуют геометрическую прогрессию, причем цифра сотен больше пяти (так как число больше 594). Можно доказать, что имеются лишь три возможности: 842, 931 и 964. Второе и третье из этих чисел нужно отбросить, так как 931 − 594 ≠ 139 и 964 − 594 ≠ 469. Остается убедиться, что для числа 842 все условия задачи выполнены.