Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

t + 2 s / x − s / y

— на столько позднее самолет вернулся в А , чем вертолет прилетел в В . Таким образом, из полученных уравнений нужно определить 1/ x и 1/ y . Умножив первое уравнение на d − s , а второе на d и сложив, найдем

( s + d ) d / x + d ( d − s )/ x + t ( d − s ) + td = 0, т. е. 2 d ²/ x = t ( s − 2 d ),

откуда

1/ x = t ( s − 2 d )/ 2 d ².

Из первого уравнения определяем 1/ y :

1/ y = 1/ x + t / d = ts / 2 d ².

Следовательно,

t + 2 s / x − s / y = t + 2 st ( s − 2 d )/ 2 d ²− ts ²/ 2 d ² = t + st ( s − 4 d )/ 2 d ².

Задача имеет решение, если все участвующие компоненты положительны. Чтобы величина 1/ x имела смысл, необходимо s > 2 d .

По условию вертолет прилетел в В раньше, чем самолет вернулся в А . Поэтому

t + st ( s − 4 d )/ 2 d ²> 0, т. е. s ² − 4 sd + 2 d ² > 0.

Получаем квадратное неравенство относительно отношения s / d :

( s / d )² − 4 s / d + 2 > 0,

откуда

s / d < 2 − √2 или s / d > 2 + √2.

Первое решение придется отбросить, так как тогда s < 2 d − √2 d , а это противоречит условию, что s > 2 d .

Ответ. t + st ( s − 4 d )/ 2 d ², s > (2 + √2) d .

18.16.Устье реки, на которой стоит порт M , обозначим через А , а устье второй реки — через В . Расстояние MA обозначим буквой x , а расстояние BN — буквой y . Искомое расстояние тогда будет равно s − ( x + y ). Путь от M до N пароход прошел за: 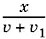ч — путь по первой реке (по течению), s − ( x + y )/ v ч — путь по озеру и 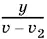ч — путь по второй реке (против течения). Так как весь путь пароход прошел за t ч, то получаем уравнение

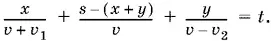
Аналогично для пути от N до M получим уравнение

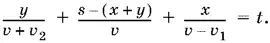
Приравнивая левые части этих уравнений, получим

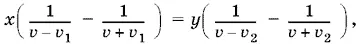
т. е.

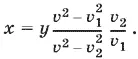
Подставим найденное выражение для x в первое уравнение и найдем

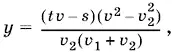
следовательно,

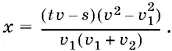
Остается найти s − ( x + y ).

Ответ.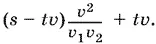

18.17.Примем расстояние AB за единицу. Пусть скорости пассажирского, курьерского и скорого поездов равны v , 2 v и u соответственно (в долях этой единицы).

Тогда время, которое находились в пути до встречи скорый и курьерский поезда, равно 1/ u + 2 v , а время до встречи скорого и пассажирского будет равно 1/ u + v . По условию

1/ u + 2 v ≥ 10½ − 8 = 5/ 2, (13)

1/ u + v − 1/ u + 2 v ≥ 1. (14)

Нам известно также, что скорый поезд преодолевает расстояние AB за 55 ч. Следовательно, за 1 ч он проходит 6/ 35 AB , т. е. u = 6/ 35. Подставим это значение u в каждое из предыдущих неравенств, находим, что, с одной стороны, v ≤ 4/ 35, а, с другой стороны, 4/ 35 ≤ v ≤ 9/ 70. Обоим неравенствам удовлетворяет единственное значение v = 4/ 35, т. е. пассажирский поезд находился в пути из В в А 8 ч 45 мин и прибыл в А в 16 ч 45 мин.

Полезно обратить внимание на то обстоятельство, что решение системы неравенств, казалось бы, упростится, если неравенства (13) и (14) сложить и заменить их суммой второе неравенство. Однако система неравенств

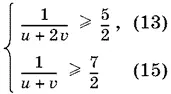
оказывается неравносильной первоначальной системе. Неравенство (15) является следствием системы (13), (14), но заменять им произвольное из исходных неравенств мы не имеем права. Система (13), (15) имеет решение v ≤ 4/ 35, в то время как решение первоначальной системы v = 4/ 35.

Ответ.16 ч 15 мин.

18.18.Пересылка одной детали в каждом из трех комплектов обходится соответственно в 2/ 7, ¼ и 7/ 25p., т. е. после приведения к общему знаменателю: 200/ 700, 175/ 700, 196/ 700p. Самой дешевой оказывается пересылка в комплектах по 40 деталей. Однако 1100 на 40 не делится и поэтому придется заказывать не только самые выгодные комплекты. Чтобы потерять как можно меньше, мы будем постепенно отказываться от самых выгодных условий, т. е. рассмотрим случаи, когда в комплекты по 40 штук укомплектованы 1080, 1040, 1000, 960, 920, ... деталей. Первый и второй случаи оказываются неосуществимыми, так как мы не сможем получить оставшиеся детали в надлежащих комплектах. Третий случай вполне допустим: он предполагает, что прибудет 25 комплектов по 40 деталей и 4 комплекта по 25 деталей. Таким образом, пересылка обойдется в 25 · 10 + 7 · 4 = 278 p. Любой другой вариант, как легко видеть, приведет к б о ́льшим расходам, поскольку количество самых выгодных комплектов уменьшится за счет увеличения количества менее выгодных комплектов (по 25 деталей) или за счет появления самых невыгодных комплектов (по 70 деталей).

Ответ.25 комплектов по 40 деталей и 4 комплекта по 25 деталей.

19.1.Сравним n −й и ( n + 1)−й члены последовательности (здесь V — знак сравнения):

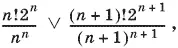
или после упрощений:

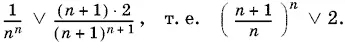
Так как

( n + 1/ n ) n = (1 + 1/ n ) n = 1 + n · 1/ n + ...,

где многоточиями обозначены некоторые положительные члены, то

( n + 1/ n ) n > 2 при n > 1.

Следовательно, последовательность убывающая, начиная со второго члена.

19.2.Так как а p , а q , а r и а s — члены арифметической прогрессии, то

a q − a р = d ( q − p ), a r − a q = d ( r − q ), a s − a r = d ( s − r ).