Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Другими словами, если мы запишем уравнение семейства кривых как уравнение относительно а , то оно имеет решение при тех и только тех значениях x и y , при которых через точку плоскости с этими координатами проходит кривая семейства. Поэтому преобразуем исходное уравнение к виду

2 a ² + 2( x − 2) а + ( x − 1)² − y = 0

и потребуем, чтобы дискриминант этого уравнения был неотрицателен

D = − х ² + 2 + 2 y ≥ 0,

откуда

y ≥ x ²/ 2 − 1.

Это необходимое и достаточное условие того, чтобы через точку ( x ; y ) проходила по крайней мере одна кривая данного семейства.

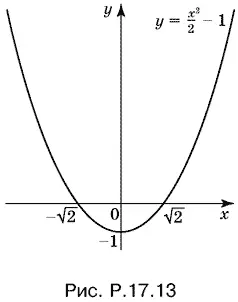
Таким образом, через все точки ( x ; y ), лежащие вне части плоскости, ограниченной параболой y = x ²/ 2− 1 (рис. P.17.13), кривые семейства не проходят. Через остальные точки кривые проходят.

18.1.Пусть x , y , z , u — производительности первой, второй, третьей и четвертой труб соответственно. Примем объем бассейна за единицу. Тогда получим систему уравнений

Вычитая из первого уравнения поочередно второе и третье, найдем соответственно

z = 1/ 12, x = 1/ 20.

Следовательно, общая производительность первой и третьей труб равна z + x = 2/ 15.

Ответ.7,5 ч.

18.2.Пусть плечи весов равны l 1и l 2соответственно. Тогда в первый раз продавец отпустил 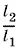кг товара, а во второй раз он отпустил 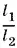кг. Таким образом, он отпустил покупателю товар массой

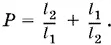
В силу неравенства между средним арифметическим и средним геометрическим

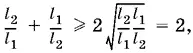
где равенство достигается лишь при l 1= l 2. Таким образом, продавец отпустил больше товара, чем следовало.

18.3.Если все 500 марок расклеить по 20 на один лист, то двух альбомов не хватит для всех марок. Поэтому 2 x < 25, т. е. x ≤ 12 ( x − количество листов в альбоме и, следовательно, целое). Если же 500 марок расклеить по 23 на один лист, то в двух альбомах окажется по крайней мере один свободный лист. Это значит, что 2 x − 1 ≥ 500/ 23, откуда 2 x ≥ 22, x ≥ 11. Итак, либо x = 11, либо x = 12.

Если в альбоме 11 листов, то y школьника было 500 − 21 · 11 = 269 марок, которые нельзя разместить на 10 листах по 23 штуки на каждом. Второе число удовлетворяет условию задачи.

Ответ.12 листов.

18.4.Поскольку понтоны находились в пути одинаковое время и в одинаковых условиях, то каждый из них проплыл одно и то же расстояние без буксира (см. второе указание на с. 203). Обозначим это расстояние через x . Каждый понтон находился в пути

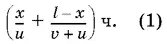
Буксир в свою очередь, помимо пути в l км вниз по течению, дважды преодолел расстояние l − 2 x км: один раз вниз по течению, другой раз вверх по течению. На весь путь y него ушло

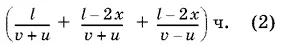
Приравниваем выражения (1) и (2) (буксир был в пути столько же времени, сколько каждый понтон) и решим уравнение.

Получим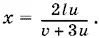

Следовательно, второй понтон должен транспортироваться на расстояние в

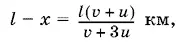
а на всю перевозку уйдет

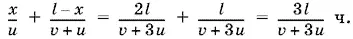
Ответ.

18.5.Пусть некто родился в 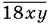году, где x − число десятков, а y — число единиц. В 1901 году ему было 1901 − 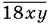лет.

Если y > 1, то, произведя вычитание, получим число 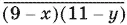, где 9 − x и 11 − y — цифры, образующие это число.

По условию сумма цифр числа 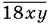равна сумме цифр числа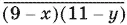

1 + 8 + x + y = (9 − x ) + (11 − y ), т. е. x + y = 5,5,

что невозможно, так как x и y — целые.

Если y ≤ 1 (это значит, что либо y = 0, либо y = 1), после вычитания получим число 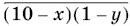, где 10 − x и 1 − y цифры, образующие это число. Когда x ≠ 0, это число состоит из двух цифр, а когда x = 0 — из трех, причем первые две цифры 1 и 0. Пусть x ≠ 0. Запишем сумму цифр для этого числа:

1 + 8 + x + y = (10 − x ) + (1 − y ), т. е. x + y = 1.

Так как x ≠ 0, то y = 0, а x = 1. Это означает, что некто родился в 1810 году.

Пусть теперь x = 0. Тогда получим уравнение

1 + 8 + y = 1 + (1 − y ),

откуда y = −3,5, что невозможно.

Ответ. В 1810 году.

18.6.Пусть одна часть имеет массу x карат, тогда другая — p − x карат. Цена этих частей равна lх ² и l ( p − x )² соответственно, где l — коэффициент пропорциональности. Так как цена целого бриллианта была равна lр ², то получим уравнение

lр ² = k [ lх ² + l ( p − x )²], которое после упрощений примет вид

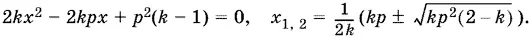
Проведем исследование.