Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

2 a − 2 = 21,

не имеющее целочисленных решений.

Можно сделать более общий вывод: если в правой части других пар уравнений типа (20) и (21) есть один нечетный множитель числа 20, то целочисленных решений y системы аналогичной (20), (21) нет. Остается рассмотреть только случаи

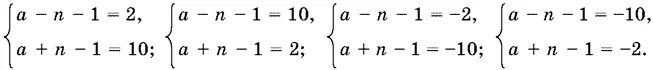
Нетрудно убедиться, что первая и вторая системы приводят к одному значению а = 7, а третья и четвертая — к значению а = −5.

При а = 7 имеем x 1= 3, x 2= 7.

При а = −5 получим x 1= −3, x 2= 1.

Ответ.−5; 7.

17.11.Обозначим x ² = y , где y ≥ 0. Получим квадратное уравнение

y ² − (1 − 2 a ) y + а ² − 1 = 0, (22)

дискриминант которого D = 5 − 4 a .

Если 5 − 4 a < 0, т. е. а > 5/ 4, решений нет.

Если 5 − 4 a = 0, т. е. а = 5/ 4, получим уравнение

y ² + 3/ 2 y + 9/ 16= 0

с единственным корнем y = −¾. Однако y ≥ 0 и потому решений тоже нет.

Пусть теперь а < 5/ 4и D > 0. Тогда уравнение (22) имеет корни:

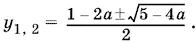
Рассмотрим сначала случаи, когда один из этих корней равен нулю, т. е.

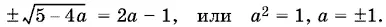
При а = −1 получим уравнение

y ² − 3 y = 0, т. е. y 1= 0, y 2= 3.

Поэтому при а = −1 исходное уравнение имеет три корня 0; −√3; √3.

При а = 1 получим

y ² + y = 0, т. е. y 1= 0, y 2= −1.

Поскольку y ≥ 0, то при а = 1 остается одно решение x = 0.

Теперь осталось рассмотреть два случая:

y 1> 0 и y 2> 0.

В первом случае нужно решить неравенство

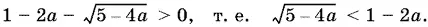
Оно равносильно системе

0 < 5 − 4 a < (1 − 2 a )²

(слева строгое неравенство, так как имеет место условие а < 5/ 4), т. е.

0 < 5 − 4 a < 1 − 4 a + 4 a ².

Правое неравенство дает нам а ² > 1. Таким образом, для y 1> 0 получим

а < −1, 1 < а < 5/ 4.

Для y 2> 0 получим

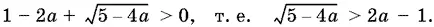
Если 2 a − 1 < 0, т. е. а < ½, то условие а < 5/ 4соблюдается. Поэтому при а < ½ получим, что у 2> 0. Если же 2 a − 1 ≥ 0, т. е. а > ½, то учтем условие а < 5/ 4. Возведя неравенство в квадрат, получим а ² < 1, т. е. во втором случае ( а ≥ ½) получим ½ ≤ а < 1. Окончательно у 2> 0 при а < 1.

Объединим решения для y 1> 0 и у 2> 0, нанеся их на числовую прямую, учтем результат, полученный для а = 5/ 4(рис. P.17.11).

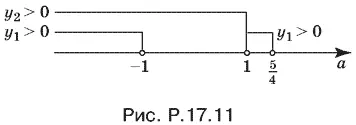
Ответ.При а < −1 уравнение относительно x имеет четыре решения. При а = −1 y него три решения, при −1 < а < 1 два решения, при а = 1 одно решение, при 1 < а < 5/ 4два решения, при а ≥ 5/ 4решений нет.

17.12.Пусть sin 4 x = y . Тогда данное уравнение преобразуется в квадратное

( a + 3) y ² + (2 a − 1) y + ( a − 2) = 0, (23)

где

| y | ≤ 1. (24)

Уравнение (23) имеет решения тогда и только тогда, когда его дискриминант неотрицателен, т. е.

D = (2 a − 1)² − 4( a + 3)( a − 2) = 25 − 8 a ≥ 0. (25)

Кроме того, нужно обеспечить, чтобы по крайней мере один из корней t 1или t 2уравнения (24) не превосходил по абсолютной величине 1.

Пусть сначала D = 0, т. е. а = 25/ 8. Тогда

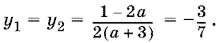
Условие (24), как мы видим, соблюдается, и уравнение sin 4 x = − 3/ 7имеет решение.

Уравнение sin z = − 3/ 7на отрезке [−π, π] имеет ровно два решения z 1и z 2. Если осуществить замену переменной: z = 4 x , то отрезок [−π, π] сузится для новой переменной x в четыре раза к началу отсчета и станет отрезком [− π/ 4, π/ 4]. Поэтому на отрезке [−π, π] для переменной x разместятся уже не 2, а 8 решений (в силу того, что sin z имеет период 2π, а sin 4 x имеет период π/ 2). Итак, а = 25/ 8— одно из искомых нами значений параметра а .

Пусть теперь D > 0, т. е. а < 25/ 8. Тогда уравнение (23) имеет два действительных решения y 1и y 2, такие, что y 1< y 2. Если оба значения y 1и y 2попадают внутрь интервала (−1, 1), то каждому значению синуса будут соответствовать два значения переменной z в интервале (−π, π) и восемь значений переменной x = z / 4в том же интервале. Решений будет ровно 8, если одно решение уравнения лежит в (−1, 1), а другое — вне этого интервала (случаи, когда y = ±1 будут рассмотрены отдельно). Конечно, можно перебрать все возможные варианты расположения y 1и y 2относительно интервала (−1, 1). Но это хлопотно и поэтому задачу следует упростить. Нас интересуют все случаи, когда один корень параболы, определяемой левой частью уравнения (23), внутри интервала (−1, 1), а другой вне этого интервала, т. е. парабола

f ( y ) = ( а + 3) y ² + (2 a − 1) y + ( а − 2) (26)

пересекает интервал (−1, 1) в одной и только в одной точке. Это условие равносильно такому

f (−1) f (1) < 0, (27)

т. е. на концах интервала (−1, 1) парабола имеет противоположные знаки. Подставим в (27) значения y = −1 и y = 1. После преобразований получим

а < 0.

При этом условии удовлетворяется и требование D > 0, т. е. требование а < 25/ 8. Итак, все значения а ∈ (−∞, 0) удовлетворяют условиям задачи, как и найденное ранее значение а = 25/ 8. Мы не рассмотрели только случаи, когда корни уравнения (23) равны −1 и 1.

Начнем со случая y 1= −1, y 2= 1, т. е. f (−1) = f (1) = 0.

Так как f (−1) = 2, f (1) = 4 a , то этот случай невозможен. Невозможен и случай, когда f (−1) = 0, так как f (−1) = 2. Остается последняя возможность: f (1) = 0. Но f (1) = 4 a . Поэтому а = 0. Уравнение (23) примет вид

3 y ² − y − 2 = 0. (28)

Уравнение (28) имеет два корня:

у 1= −⅔ и y 2= 1.

Первому из них уже будут соответствовать два значения z и восемь значений x на отрезке [−π, π]. Сколько соответствует второму, не существенно. Достаточно, что не меньше одного. Поэтому этот случай не дает новых значений параметра а .

Ответ. а ∈ (−∞, 0) ∪ ( 25/ 8).

17.13.Через точку на плоскости ( x ; y ) с фиксированными координатами x и y проходит кривая семейства тогда и только тогда, когда существует значение параметра а , удовлетворяющее данному уравнению кривых семейства при этих фиксированных x и y .