Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

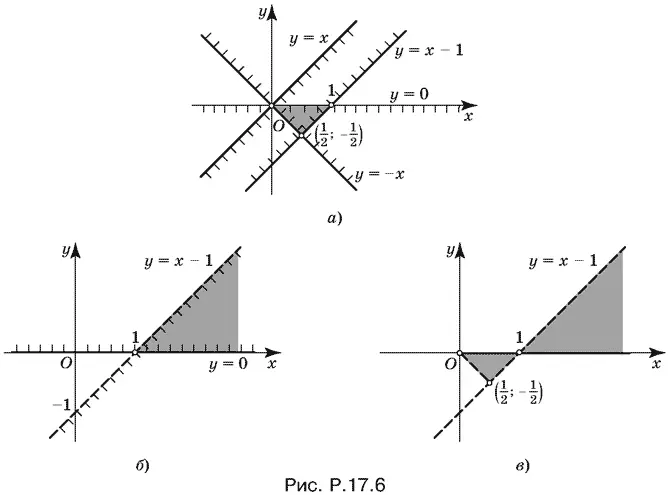
Внимание! Интервалы оси абсцисс (0, 1) и (1, +∞) принадлежат множеству решений. Остальные точки границы ему не принадлежат.

17.7.Найдем решения неравенства

( x − | x |)² + ( y − | y |)² ≤ 4 (17)

для каждого квадранта отдельно.

Пусть одновременно x ≥ 0, y ≥ 0. Тогда | x | = x , | y | = y . Неравенство (17) приобретет вид 0 ≤ 4, т. е. оно удовлетворяется при всех x и y из первого квадранта.

Когда x ≤ 0, y ≥ 0, точки ( x , y ) лежат во втором квадранте и на его границе. Тогда | x | = − x , | y | = y и неравенство (17) приобретет вид

(2 x )² ≤ 4, т. е. x ² ≤ 1, или −1 ≤ x ≤ 0,

так как мы рассматриваем значения x ≤ 0. Это будет полоса шириной 1, расположенная во втором квадранте параллельно оси Оу (рис. P.17.7).

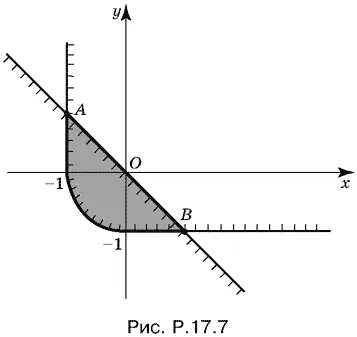
Аналогично в четвертом квадранте получим полосу шириной 1 параллельную оси Ox .

В четвертом квадранте x ≤ 0, y ≤ 0 и мы получим из (17) неравенство

х ² + y ² ≤ 1,

т. е. ему удовлетворяют точки четвертого квадранта, лежащие внутри и на границе круга x ² + y ² = 1.

Нанесем на рис. P.17.7 точки прямой y = − x . Значения, удовлетворяющие неравенству x + y ≤ 0, будут лежать под этой прямой и на ней. Нас интересует площадь фигуры, покрытой штриховкой. Эта фигура состоит из двух прямоугольных треугольников с катетами 1 (в сумме они образуют квадрат со стороной 1) и четверти круга, имеющего радиус 1.

Ответ.1 + π/ 4.

17.8.Уравнение прямой, проходящей через точки В и D , имеет вид y = 8 − x , а уравнение прямой AC есть 2 y = x + 4. Решая эти два уравнения в системе, найдем x = y = 4, т. е. E (4; 4).

Проведем все построения, описанные в указании II на с. 201 (рис. P.17.8).

Дополнительно проведем ЕL || CK , где L ∈ HK , CK ⊥ HK , F — точка пересечения HK и Оу . Искомая площадь может быть определена так:

S ABCDE = S FGCK − S CKD − S ELD − S ELH + S AFH − S AGB .

Каждый из треугольников — прямоугольный с известными катетами.

Ответ.36.

17.9.Пусть x + y = u , y − x = v . Тогда

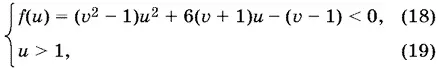
а множество решений этой системы проецируется на прямую u = 2. Другими словами, нас интересуют все значения v , при каждом из которых система неравенств (18), (19) имеет хотя бы одно решение. Пусть u — независимая переменная. Она будет абсциссой, а f ( u ) — ординатой для исследуемой нами плоскости. Величина v — параметр. График функции f ( u ) — парабола, если v ² − 1 ≠ 0. Она обращена ветвями вверх при v ² − 1 > 0 и ветвями вниз при v ² − 1 < 0. Отдельно нужно рассмотреть случай v ² − 1 = 0.

Итак, перед нами три случая.

1. v ² − 1 < 0, т. е. −1 < v < 1. Парабола обращена ветвями вниз. При достаточно больших значениях u > 1 она принимает отрицательные значения. Поэтому в плоскости ( u , v ) в проекции на прямую u = 2 мы получим интервал −1 < v < 1.

2. v ² − 1 = 0. Если v = −1, то f ( u ) ≡ 2 и отрицательных решений нет. Если v = 1, то f ( u ) = 12 u , где u > 1. Отрицательных значений, удовлетворяющих системе (18), (19), в этом случае тоже нет.

3. Когда v ² − 1 > 0, т. е. либо v < −1, либо v > 1 ветви параболы обращены вверх. Правее прямой u = 1 парабола может принимать отрицательные значения в двух случаях:

а) уравнение f ( u ) = 0 имеет два корня, и при этом абсцисса u 0вершины ( u 0; v 0) параболы превосходит 1, т. е.

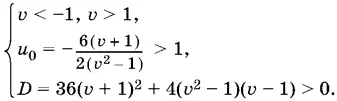
После простых преобразований:

Окончательно получим

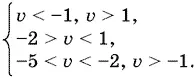
Система не имеет решений, так как одновременно все три ограничения не удовлетворяются;

б) абсцисса u 0вершины ( u 0; v 0) не больше 1, но f (1) меньше нуля:

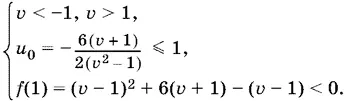
После преобразований получим

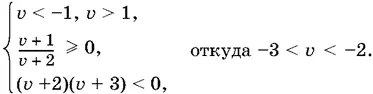
Обобщим все рассмотренные варианты. Условиям удовлетворяют два интервала значений v , проекции которых в плоскости ( u , v ) на прямую u = 2 не пересекаются:

v ∈ (−3, −2) ∪ (−1, 1).

Когда мы вернемся к переменным x и y , ситуация не изменится, так как замена

не ведет к изменению расстояний между соответственными точками в старой и новой системе координат.

Основная трудность этой задачи состояла в том, что исследование пришлось вести одновременно в двух плоскостях ( u , f ( u )) и ( u , v ). К тому же, в конечном счете, нас интересует третья плоскость ( x , y ).

Ответ.2.

17.10.Если x 1и x 2— целочисленные корни данного уравнения, то x 1+ x 2= а + 3, откуда следует, что а = x 1+ x 2− 3 — целое число. Корни данного уравнения равны

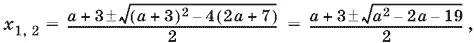
отсюда

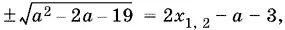
т. е. 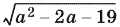— целое число. Тогда

а ² −2 a + 1 = п ² + 20, т. е. ( а − 1)² − п ² = 20,

или

( а − n − 1)( а + n − 1) = 20.

Остается рассмотреть варианты, когда каждая из скобок равна целочисленным множителям числа 20. Начнем со случая

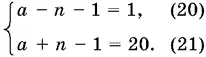
Сложив эти два уравнения, получим уравнение