Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. x = 2.

15.10.Обозначим первый сомножитель через А , а второй через В , тогда данное неравенство равносильно совокупности двух систем

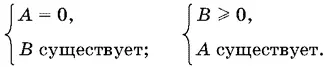
При А = 0 получаем x = 1. Так как при x = 1 В не существует, то первая система не имеет решений.

Перейдем теперь ко второй системе. Для решения неравенства

log tg x (2 + 4 cos² x ) ≥ 2

нет необходимости рассматривать случай 0 < tg x < 1, так как А не существует при этих значениях tg x . Если же x > 1, то получим

2 + 4 cos² x ≥ tg² x . (1)

Выражаем tg² x через cos² x (равносильность при такой замене не нарушается):

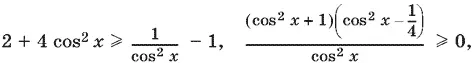
т. е. cos² x ≥ ¼, или

cos x ≤ −½, cos x ≥ ½.

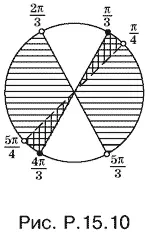
Нанесем решения этих неравенств на тригонометрический круг (рис. P.15.10). Приняв во внимание условие tg x > 1, получим решение системы.

Ответ. π/ 4+ π k < x ≤ π/ 3+ π k .

16.1.Из неравенства между средним арифметическим и средним геометрическим немедленно следует, что правая часть данного уравнения не меньше двух. Однако его левая часть не может стать больше двух. Поэтому остается лишь одна возможность:

Последнее равенство достигается лишь при x ² = 1, т. е. при x = ±1. Подставляя эти значения в левую часть первого уравнения, получим

2 sin² ½ sin² 1/ 6< 2.

Таким образом, исходное уравнение не имеет решений.

16.2.Так как 1/ cos² x = tg² x + 1, то уравнение можно переписать в виде

2 2 tg² x + 2 · 2 tg² x − 80 = 0,

откуда

2 tg² x = 8, tg² x = 3, tg x = ±√3, x = n π ± π/ 3

(второе уравнение 2 tg² x = −10 не имеет решений).

Ответ. n π ± π/ 3.

16.3.Так как в условие одновременно входят tg x и etg x , то мы можем воспользоваться неабсолютным тождеством ctg x = 1/ tg x , не опасаясь нарушения равносильности. Получим уравнение

(tg x ) sin x = (tg x ) −cos x .

Если tg x < 0, то sin x и cos x − дробные числа, и обе части равенства теряют смысл. При tg x = 0 и sin x обращается в нуль, т. е. левая часть теряет смысл.

Если tg x > 0, но ≠ 1, то sin x = −cos x , откуда tg x < 0, что противоречит сделанному предположению. Остается tg x = 1, x = (4 k + 1) π/ 4.

Ответ.(4 k + 1) π/ 4.

16.4.Данное уравнение можно записать так:

sin (2 x + 2 x − 1) = ½,

откуда

2 x + 2 x − 1= n π + (−1) n π/ 6, или 2 x = 2 n π/ 3+ (−1) n π/ 9.

Какое бы положительное число ни стояло в правой части, уравнение будет иметь решение.

Неравенство

2 n π/ 3+ (−1) n π/ 9> 0

выполняется при n ≥ 0.

Ответ. log 2[ 2 n π/ 3+ (−1) n π/ 9], где n ≥ 0.

16.5.Уравнение можно переписать так:

lg sin x + lg sin 5 х + lg cos 4 x = 0,

или в виде системы

Из первого уравнения следует, что |sin x | = 1, |sin 5 х | = 1, |cos 4 x | = 1 одновременно. С учетом ограничений придем к системе

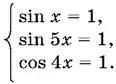
Из первого уравнения x = π/ 2 + 2π n . Подставляем во второе и третье уравнения:

sin [5( π/ 2+ 2π n )] = sin π/ 2= 1, cos [4( π/ 2+ 2π n )] = cos 0 = 1.

Ответ. π/ 2+ 2π n .

16.6.Обозначив lg (sin x + 4) = y , получим уравнение

y ² + 2 y − 5/ 4= 0,

y которого два корня: y 1 = − 5/ 2, y 2= ½.

Для первого корня получим

lg (sin x + 4) = − 5/ 2,

откуда

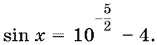
Так как 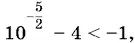то соответствующих значений x нет.

Для второго корня получим

lg (sin x + 4) = ½,

откуда

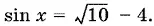
Так как то можем найти x .

Ответ.

16.7.Данное уравнение эквивалентно системе

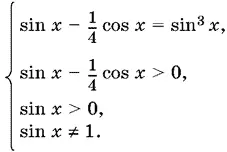
Уравнение можно преобразовать, если сгруппировать sin x и sin³ x :

sin x (1 − sin² x ) − ¼ cos x = 0, или sin x cos² x − ¼ cos x = 0.

Так как sin x > 0, то cos² x < 1, и любое решение уравнения

sin x cos² x − ¼ cos x = 0

удовлетворяет неравенству

sin x − ¼ cos x > 0.

Запишем уравнение в виде

cos x (sin 2 x − ½) = 0.

Так как sin x ≠ 1 и sin x > 0, то cos x ≠ 0. Остается

sin 2 x = ½,

откуда

x 1 = π n + π/ 12, x 2 = (2 n + 1) π/ 2− π/ 12.

Из всех ограничений осталось удовлетворить только одному: sin x > 0. Чтобы добиться этого, нужно для x 1и x 2взять n = 2 k .

Ответ.2π k + π/ 12; 2π k + 5π/ 12.

16.8.Данное уравнение равносильно системе

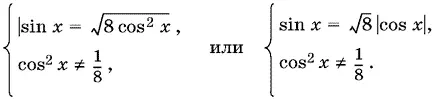
Условие sin x > 0 содержится в уравнении, так как справа стоит всегда неотрицательное число, а если cos x = 0, то sin x ≠ 0.

Рассмотрим следствие исходного уравнения

sin x = ±√8 cos x ,

а в конце проверим выполнение условий: sin x > 0 и cos² x ≠ 1/ 8. Получим

tg x = ±√8, x = n π + arctg √8.

Если tg x = ±√8, то tg² x + 1 = 9 и cos² x = 1/ 9 ≠ 1/ 8. Чтобы проверить выполнение условия sin x > 0, рассмотрим два случая.

Если n = 2 k , то x = 2 k π ± arctg √8. Это — углы, лежащие в первой и четвертой четвертях; условие sin x > 0 выполняется лишь для тех из них, которые лежат в первой четверти: x 1 = 2 k π + arctg √8.

Если n = 2 k + 1, то x = 2 k π + π ± arctg √8. Здесь нужно выбрать знак минус, так как только тогда мы получаем угол, лежащий во второй четверти.