Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Неравенство относительно y перепишем в виде
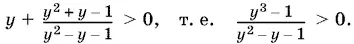
После разложения левой части на множители получим
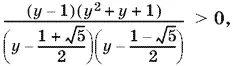
откуда 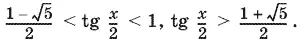
Находим интервалы изменения x :
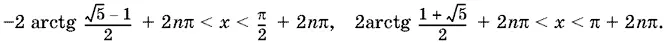
Остается выделить решения, лежащие в интервале 0 < x < π.
Ответ. 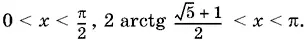
14.15.Выразив sin 3α и cos 2α через sin α и обозначив sin α = y , получим
4(3 y − 4 у ³) + 5 ≥ 4 − 8 у ² + 5 у ,
или
16 у ³ − 8 у ² − 7 у − 1 ≤ 0.
Нетрудно заметить, что y = 1 — корень многочлена, стоящего в левой части неравенства. Теперь можно разложить этот многочлен на множители:
16 у ³ − 8 у ² − 7 у − 1 = ( y − 1)(4 у + 1)².
Так как y = sin α, то y − 1 ≤ 0, а следовательно, и многочлен 16 у ³ − 8 у ² − 7 y − 1 неположителен, что доказывает неравенство.
14.16.Значения x = π k , при которых sin x = 0, являются решениями неравенства при всех а > 0. На множестве остальных точек данное неравенство равносильно такому:
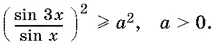
Так как
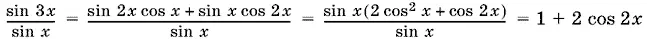
(сокращение на sin x правомерно, так как рассматриваются точки, в которых sin x ≠ 0), то приходим к неравенству:
(1 + 2cos 2 x )² ≥ а ².
Так как а > 0, то это неравенство распадается на два:
1 + 2cos 2 x ≤ − а , 1 + 2cos 2 x ≥ а ,
т. е.
cos 2 x ≤ − a + 1/ 2, cos 2 x ≥ a − 1/ 2.
Первое имеет решения при − a + 1/ 2 ≥ −1, а второе — при a − 1/ 2 ≤ 1 или соответственно а ≤ 1 и а ≤ 3.
Найдем решение неравенства cos 2 x ≤ − a + 1/ 2. Так как а > 0, то правая часть неравенства отрицательна и при а < 1 ему будут удовлетворять углы 2 x , подвижные радиусы которых лежат в секторе, расположенном во второй и третьей четвертях симметрично горизонтальной оси (сделайте рисунок самостоятельно), т. е.
arccos (− a + 1/ 2) + 2π k ≤ 2 x ≤ −arccos (− a + 1/ 2) + 2π + 2π k .
Так как arccos (− y ) = π − arccos y , то
π − arccos a + 1/ 2+ 2π k ≤ 2 x ≤ arccos a + 1/ 2− π + 2π + 2π k .
Результат окончательных преобразований дан в ответе.
Ответ.При любом а > 0 y неравенства есть решения x = π k ; при 0 < а ≤ 3 появляется вторая серия решений:
−½ arccos a − 1/ 2+ π k ≤ x ≤ ½ arccos a − 1/ 2+ π k ;
при 0 < а ≤ 1 — третья серия:
−½ arccos a + 1/ 2+ π/ 2(2 k + 1) ≤ x ≤ ½ arccos a + 1/ 2+ π/ 2(2 k + 1).
14.17.Обозначим cos t = z и преобразуем условие задачи в неравенство
2 z ² + (2 cos x cos y ) z + ½ cos² x cos² y + cos x − cos y > 0,
которое должно удовлетворяться при всех −1 ≤ z ≤ 1. Парабола, соответствующая трехчлену, стоящему в левой части неравенства, имеет абсциссу
z 0= −½ cos x cos y .
Следовательно, −1 < z 0< 1. Таким образом, условие задачи равносильно требованию, чтобы ордината этой вершины была положительна, что в свою очередь сводится к требованию отрицательности дискриминанта:
D = cos² x cos² y − cos² x cos² y − 2(cos x − cos y ) < 0,
т. е.
cos x − cos y > 0, sin x + y / 2sin y − x / 2> 0. (2)
Нанесем на график точки, в которых
sin x + y / 2sin y − x / 2= 0.
Это будет совокупность прямых
x + y = 2π k , y − x = 2π n ,
параллельных биссектрисам первого и второго координатных углов (рис. P.14.17), пересекающих оси координат в точках, координаты которых кратны 2π. Сами эти прямые не удовлетворяют неравенству (2), однако они разбивают всю плоскость на квадраты, внутри каждого из которых произведение sin y + x / 2sin y − x / 2сохраняет постоянный знак.

Рассмотрим квадрат ОАВС , примыкающий к началу координат снизу. Для всех внутренних точек этого квадрата
sin y + x / 2< 0 и sin y − x / 2< 0,
т. е. неравенство (2) удовлетворяется. При переходе через границу квадрата в любой точке, кроме вершины, произойдет смена знака одного из сомножителей. При переходе же через вершину знак поменяется дважды. Таким образом, вся плоскость окажется разбитой на области, расположенные в шахматном порядке. Те области, в которых неравенство (2) удовлетворяется, заштрихованы.
Ответ. 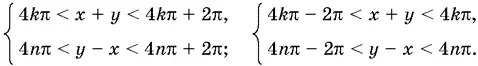
Глава 15
Трансцендентные неравенства
15.1.Данное неравенство равносильно такому:
(log sin x 2)² < 2 log sin x 2 + 3.
Обозначив log sin x 2 = y , получим
y ² − 2 y − 3 < 0,
откуда
−1 < y < 3, или −1 < log sin x 2 < 3.
Последнее неравенство эквивалентно системе
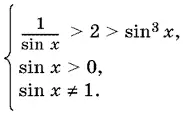
Первое из неравенств системы можно переписать так: 0 < sin x < ½·
Ответ.2 n π < x < π/ 6+ 2 n π; 5π/ 6+ 2 n π < x < π + 2 n π.
15.2.Пусть tg x = √ y . Тогда sin² x = y / 1 + y , и данное неравенство можно переписать в виде

(докажите, что последнее преобразование не нарушает равносильности). При 0 < y < 1 и y > 1 получаем различные системы:
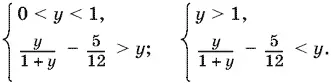
Их можно объединить в одну:

Второе неравенство можно решить методом интервалов
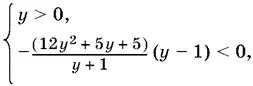
т. е. y > 1.
Итак, tg² x > 1, причем tg x > 0.
Читать дальшеИнтервал:
Закладка:










