Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Таким образом, уравнение примет вид:

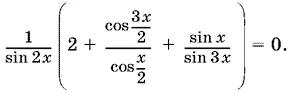
После сложения дробей в скобках получим числитель, который, шаг за шагом, преобразуем:

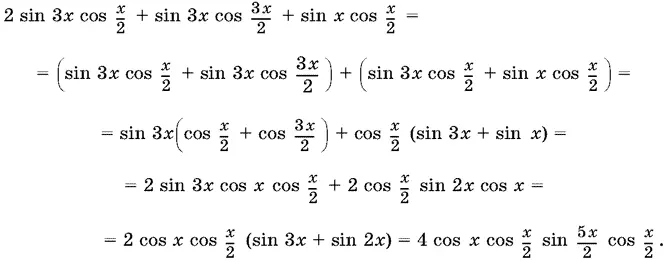
Итак, данное уравнение преобразовано к равносильному ему:

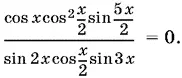
Нужно найти корни числителя, при которых знаменатель не обращается в нуль. Сомножитель cos x ≠ 0, так как в знаменателе есть sin 2 x = 2 sin x cos x . Второй сомножитель тоже не равен нулю, так как входит множителем и в числитель, и в знаменатель. Остается sin 5 x / 2= 0, что имеет место при 5 x / 2= π k , т. е. при x = 2π k / 5, где k = 0, ±1, ±2.

Отсеим из этого множества чисел значения, при которых знаменатель обращается в нуль. Это будет, когда k делится на 5, т. е. k = 5 n .

При остальных k , т. е. при k = 5 n ± 1 и k = 5 n ± 2 знаменатель в нуль не обращается.

Ответ.2π (5 n ± 1)/ 5, 2π (5 n ± 2)/ 5.

13.51.Ограничения sin t ≠ 0 и cos t ≠ 0 объединяет условие sin 2 t ≠ 0. Учтем, что

sin 3 t − sin t = 2 sin t cos 2 t , ctg² t + 1 = 1/ sin² t .

Тогда уравнение (мы учли, что sin 2 t ≠ 0) примет вид

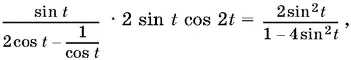
или

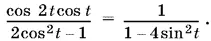
Так как 2 cos² t = 1 + cos 2 t , а 2 sin² t = 1 − cos 2 t , то после сокращения дроби в левой части уравнения на cos 2 t получим

cos t = 1/ 2 cos 2 t − 1,

где cos 2 t ≠ 0.

Если cos 2 t ≠ ½, то

2 cos 2 t cos t − cos t = 1,

или

cos 3 t + cos t − cos t = 1,

т. е. cos 3 t = 1 и t = 2π k / 3, k = 0, ±1, ±2, ... .

Остается учесть все ограничения:

sin 2 t ≠ 0, cos 2 t ≠ 0, cos 2 t ≠ ½.

Условия sin t ≠ 0, cos t ≠ 0, cos 2 t ≠ 0 можно объединить: sin 4 t ≠ 0. Из значений неизвестного t = 2π k / 3 нужно исключить те, при которых имеет место одно из равенств: sin 4 t = 0 или cos 2 t = ½. Первое равенство будет иметь место, когда k делится на 3, т. е. k = 3 n . Остаются две возможности: k = 3 m + 1 и k = 3 m − 1. Итак, остались для проверки значения:

t = 2π (3 m + 1)/ 3 и t = 2π (3 m − 1)/ 3.

Среди них не должно быть таких, что cos 2 t = 1. Вычислим cos[2π (3 m + 1)/ 3] и cos[2π (3 m − 1)/ 3]

cos[2π (3 m + 1)/ 3] = cos (2π m + 2π/ 3) = cos 2π/ 3= −½,

cos[2π (3 m − 1)/ 3] = cos (2π m − 2π/ 3) = cos (− 2π/ 3) = −½.

Ответ.2π (3 m ± 1)/ 3.

14.1.Неравенство равносильно такому:

sin² x > cos² x ,

т. е.

cos² x − sin² x < 0, cos 2 x < 0,

откуда

π/ 2 + 2 n π < 2 x < 3π/ 2+ 2 n π.

Ответ. π/ 4+ n π < x < 3π/ 4+ n π.

14.2.Перепишем неравенство в виде

1/ √2cos x − 1/ √2sin x < − 1/ √2,

откуда

cos ( x + π/ 4) < − 1/ √2,

т. е.

3π/ 4+ 2 n π < x + π/ 4< 5π/ 4+ 2 n π

Ответ. π/ 2+ 2 n π < x < π + 2 n π.

14.3. Способ 1.Неравенство sin x < 3 cos x равносильно совокупности трех систем

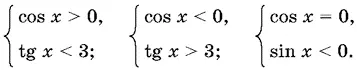
Решение каждой из них изображено на рис. P. 14.3.

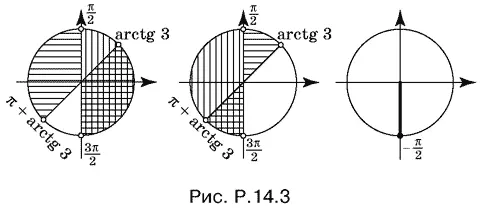
Способ 2.Запишем данное неравенство так:

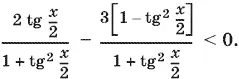
При использовании этих формул мы исключили из области существования левой части неравенства точки, в которых tg x / 2не существует. Поэтому нужно подставить в исходное неравенство x = π(2 n + 1). Убеждаемся, что

sin π(2 n + 1) − 3 cos π(2 n + 1) = 3,

т. е. эти точки не являются корнями неравенства.

Приходим к квадратному неравенству

3 tg² x / 2+ 2 tg x / 2− 3 < 0,

откуда

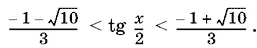
Наиболее компактный ответ получается при решении неравенства первым способом.

Ответ.arctg 3 + π(2 n + 1) < x < arctg 3 + 2π n .

14.4.Поскольку tg x входит в правую часть данного неравенства, замена sin 2 x и cos 2 x их выражениями через tg x приведет к равносильному неравенству. Обозначив tg x = y , получим

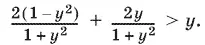
Так как 1 + y ² > 0, то это неравенство равносильно такому:

y ³ + 2 y ² − y − 2 < 0.

Сгруппировав первый член с третьим, а второй с четвертым, разложим левую часть на множители:

( y + 2)( y + 1)( y − 1) < 0.

Решения этого неравенства будут лежать в интервалах

y < −2, −1 < y < 1,

т. е.

tg x < − 2, −1 < tg x < 1.

Ответ.− π/ 2+ n π < x < −arctg 2 + n π; − π/ 4+ n π < x < π/ 4+ n π.

14.5. Способ 1.Неравенство равносильно совокупности двух систем

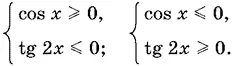
Начнем со второго неравенства. При решении обеих систем нам понадобятся радиусы, на которых tg 2 x = 0 и tg 2 x не существует, так как только в этих точках может произойти перемена знака.

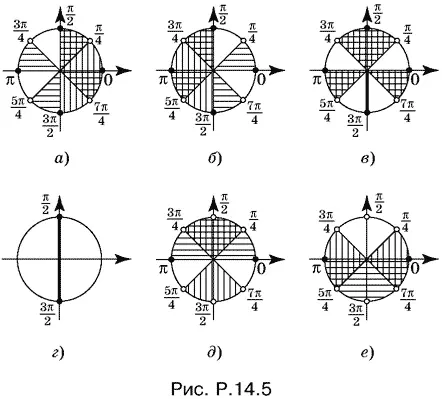
Эти радиусы нанесены на рис. P.14.5, а и б , причем на первом горизонтальной штриховкой заштрихованы те секторы, где tg 2 x < 0, а на втором — остальные секторы круга. Остается в первом случае выбрать секторы, в которых cos x ≥ 0, а во втором — в которых cos x ≤ 0.

Нанесем решения данного неравенства на общий чертеж (рис. P.14.5, в ), после чего можно записать ответ.

Способ 2.Воспользуемся формулой тангенса двойного угла и перепишем неравенство в виде

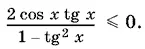
Формула, которую мы применили, является неабсолютным тождеством, так как в результате ее использования из области определения левой части неравенства исчезают значения x , при которых cos x = 0. Непосредственной подстановкой в исходное неравенство убеждаемся, что x = π/ 2+ k π — его корни. Отметив соответствующие радиусы на чертеже (рис. P.14.5, г ), можем считать, что cos x ≠ 0, и решать неравенство