Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Следовательно,

sin ( x − y ) = 2 a + cos ( x + y ) = ½ − 2 a ² = 1 − 4 a ²/ 2.

Прежде чем решать систему

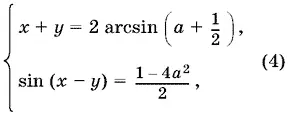
выясним, при каких а она имеет решение.

Первоначальная система накладывает на параметр а такие ограничения: | а | ≤ 1, | а + ½| ≤ 1, где первое — следствие того, что в левой части первого уравнения стоит произведение синуса и косинуса, а второе — следствие определения арксинуса.

Поскольку при преобразованиях исходной системы равносильность не нарушалась, то нет необходимости учитывать первоначальные ограничения, так как они будут содержаться в ограничениях системы (4):

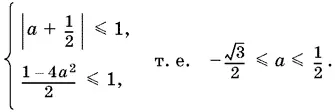
Итак, если параметр а лежит на интервале − √3/ 2 ≤ а ≤ ½, то систему (4) можно переписать в виде

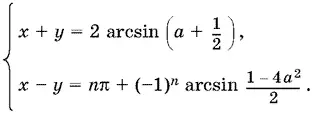
Решая эту систему, найдем x и y . Остается сделать проверку.

Ответ.При − √3/ 2≤ а ≤ ½

13.39.Обозначим tg² x = u , tg² y = v . Тогда в левой части уравнения получим u ² + v ² + 2/ uv . Это выражение не может стать меньше, чем 2 uv + 2/ uv , так как u ² + v ² ≥ 2 uv . Выражение 2 uv + 2/ uv тоже легко оценить:

2[ uv + 1/ uv ] ≥ 4,

причем равенство в первом и во втором случаях достигается лишь при u = v = 1.

Таким образом, сумма, стоящая в левой части равенства, не может стать меньше 4, в то время как правая часть этого равенства не может превзойти 4. Остается единственная возможность: обе части равенства одновременно равны 4. Получаем систему

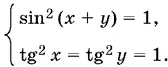
Второму уравнению удовлетворяют значения x = ± π/ 4+ k π, y = ± π/ 4+ n π, где знаки берутся в произвольных сочетаниях. Однако первое уравнение будет удовлетворяться только в том случае, когда в выражениях для x и y взяты одинаковые знаки.

Ответ.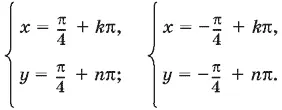

13.40. Способ 1.Умножив sin² x на sin² 3 x + cos² 3 x = 1 и сгруппировав члены, содержащие sin² 3 x , получим

sin² x cos² 3 x + sin² 3 x (sin² x − sin x + ¼) = 0,

или

sin² x cos² 3 x + sin² 3 x (sin x − ½)² = 0.

Последнее уравнение эквивалентно системе

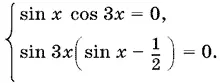
Корни первого уравнения найти нетрудно:

x 1— n π, x 2= π/ 6+ n π/ 3.

Подставляя x 1во второе уравнение, убеждаемся, что оно удовлетворяется при этих значениях неизвестного. Подставляя во второе уравнение x 2, получим

sin ( π/ 2+ n π) [sin ( π/ 6+ n π/ 3) − ½] = 0.

Так как первый сомножитель никогда не обращается в нуль, то последнее равенство можно записать так:

sin ( π/ 6+ n π/ 3) = sin π/ 6.

Воспользовавшись условием равенства синусов (если sin α = sin β, то либо α − β = 2 k π, либо α + β = (2 k + 1)π), получим

π/ 3+ n π/ 3= (2 k + 1)π, откуда n = 6 k + 2,

и

n π/ 3= 2 k π, откуда n = 6 k .

Таким образом,

x 1= n π, x 2= π/ 6+ 2 k π, x 3= 5π/ 6+ 2 k π.

Способ 2.Перепишем уравнение в виде

4 sin² x − 4 sin x sin² 3 x + sin² 3 x = 0,

т. е.

(2 sin x − sin² 3 x )² + (sin² 3 x − sin 43 x ) = 0.

Так как оба слагаемых неотрицательны, то

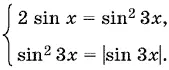
Из второго уравнения получим: либо sin 3 x = 0 и x = n π/ 3, либо |sin 3 x | = 1 и x = π/ 6+ n π/ 3. Остается отобрать из этих решений те, которые удовлетворяют первому уравнению, что делается так же, как и в первом способе решения.

Способ 3.Рассмотрим данное уравнение как квадратное относительно sin x . Тогда

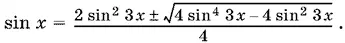
Чтобы уравнение имело действительные решения, необходимо и достаточно потребовать неотрицательности дискриминанта

sin² 3 x (sin² 3 x − 1) ≥ 0.

Выражение в скобках не может стать положительным. Следовательно, остается лишь две возможности: либо sin² 3 x = 0, либо sin² 3 x = 1. Если sin² 3 x = 0, то, подставляя в первоначальное уравнение, получим sin² x = 0, т. е. x = π k . Если sin² 3 x = 1, то придем к квадратному уравнению

sin² x − sin x + ¼ = 0, откуда sin x = ½.

Ответ. n π; π/ 6+ 2 k π; 5π/ 6+ 2 k π.

13.41. Способ 1.Преобразовав данное уравнение к функциям от x + y / 2и x − y / 2и дополнив полученное таким образом выражение до полного квадрата, придем к уравнению вида

(2 cos x + y / 2− cos x − y / 2)² + sin² x − y / 2= 0.

Это уравнение эквивалентно системе

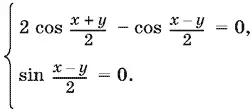
Решая второе уравнение системы, найдем

x − y / 2= n π,

откуда x − y = 2 n π, а x = y + 2 n π.

Подставляя найденное выражение для x в первое уравнение, получим

2 cos ( y + n π) − cos n π = 0.

Число n может быть либо четным, либо нечетным. Если n = 2 k , то уравнение примет вид 2 cos y − 1 = 0, откуда cos y = ½.

При n = 2 k + 1 получим −2 cos y + 1 = 0, откуда снова cos y = ½. Таким образом,

y = 2π m ± π/ 3, а x = y + 2 n π = 2π( n + m ) ± π/ 3.

В этом случае n + m можно рассматривать как новое целочисленное переменное и записать ответ следующим образом:

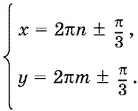
Способ 2.Преобразовав уравнение к виду A cos y + В sin y = 3/ 2− cos x , где A = 1 − cos x , В = sin x (причем A и В не равны нулю одновременно), оценим его левую часть

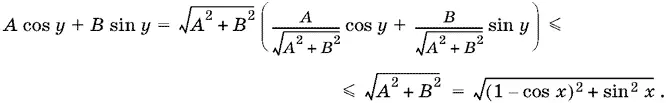
Чтобы данное уравнение имело решение, необходимо, чтобы

(1 − cos x )² + sin² x ≥ ( 3/ 2− cos x )²

или

cos² x − cos x + ¼ ≤ 0, т. е. (cos x − ½) ≤ 0.

Так как квадрат некоторого выражения не может быть отрицательным, то cos x = ½, откуда