Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

x = 2 n π ± π/ 3.

Чтобы найти y , можно подставить найденные значения x в исходное уравнение. Однако достаточно заметить, что исходное уравнение симметрично относительно x и y . Следовательно, для второго неизвестного мы тоже получим

y = 2 m π ± π/ 3.

Остается установить соответствие между найденными значениями x и y , что легко сделать проверкой, так как здесь нужно рассмотреть всего четыре различные возможности. Убеждаемся, что из четырех возможностей уравнению удовлетворяют только две, когда для x и y выбраны одинаковые знаки.

Ответ. x = 2 n π ± π/ 3, y = 2 m π ± π/ 3; где берутся либо только верхние, либо только нижние знаки.

13.42. Способ 1.Задача сводится к отысканию таких а и b , при которых равенство

tg x + tg ( а − x ) + tg x tg ( а − x ) = b является неабсолютным тождеством. Обозначив tg x = z и tg а = с (в предположении, что а ≠ π/ 2(2 n + 1)), получим

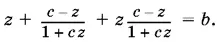
Перенеся все в левую часть и приведя к общему знаменателю, получим

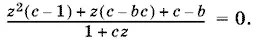
Это уравнение относительно z является неабсолютным тождеством тогда и только тогда, когда многочлен, стоящий в числителе, обращается в нуль при всех z , кроме, быть может, одного значения z , обращающего в нуль знаменатель левой части, что равносильно тождественному равенству нулю этого многочлена. Так как условием тождественного равенства многочлена нулю является равенство нулю всех его коэффициентов, то получим с = 1, b = 1, т. е. b = 1, а = π/ 4+ k π. Случай а = (2 n + 1) π/ 2 приводит к равенству tg x + ctg x = b − 1, которое является неабсолютным тождеством.

Способ 2.Равенство

tg x + tg ( а − x ) + tg x tg ( а − x ) = b

должно удовлетворяться тождественно по отношению к x . Положив x = 0, получим, что либо tg а = b , либо tg а не существует, т. е. а = (2 n + 1) π/ 2. Аналогично для x = π/ 4получим, что либо tg ( а − π/ 4) = b − 1/ 2, либо а − π/ 4= π/ 2+ π n , т. е. а = 3π/ 4+ π n .

Итак, если а ≠ (2 n + 1) π/ 2и а ≠ 3π/ 4+ π n , то получаем систему, которой должны удовлетворять а и b :

tg а = b , tg ( а − π/ 4) = b − 1/ 2.

Заменив во втором уравнении b на tg а , перепишем его в виде

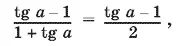
откуда tg а = 1. Таким образом, b = 1, а = π/ 4+ n π. Проверим, будет ли при этих значениях а и b равенство, написанное в начале решения, неабсолютным тождеством. После подстановки получим

tg x + tg ( π/ 4+ n π − x ) + tg x tg ( π/ 4+ n π − x ) = 1

или

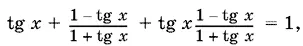
т. е. равенство

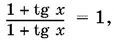
являющееся неабсолютным тождеством.

Остается рассмотреть исключенные значения параметра а . Если а = (2 n + 1) π/ 2, то приходим к равенству tg x + ctg x = b − 1, являющемуся неабсолютным тождеством. Когда а = 3π/ 4+ π n , то tg а = −1 и, следовательно, b = tg а = −1. При этом исходное равенство принимает вид

tg x + ctg ( x − π/ 4) + tg x ctg ( x − π/ 4) = −1.

Оно является неабсолютным тождеством, так как при π/ 4< x < π/ 2функции tg x и ctg ( x − π/ 4) положительны, а потому левая часть равенства не может быть равна −1.

Ответ. а = π/ 4+ n π, b = 1.

13.43.Оценим левую часть уравнения:

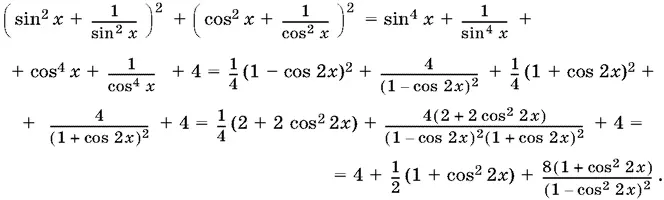
С увеличением cos² 2 x это выражение растет. Поэтому оно будет достигать своего минимума, когда cos² 2 x = 0. Таким образом, левая часть уравнения не может стать меньше 12,5.

Поскольку правая часть не может превзойти 12,5, то получаем систему

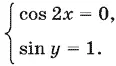
Ответ.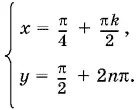

13.44.Представив данное уравнение в виде

sin 2 x − sin x cos 2 x = 3/ 2,

оценим левую часть. Чтобы оценить выражение

A sin 2 x + В cos 2 x ,

его нормируют, т. е. представляют в виде

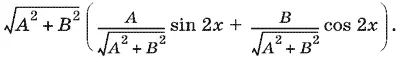
Выражение, стоящее в скобках, можно записать как sin (2 x + α), т. е. оно не превосходит по абсолютной величине единицу. В нашем случае A = 1, В = −sin x . Поэтому

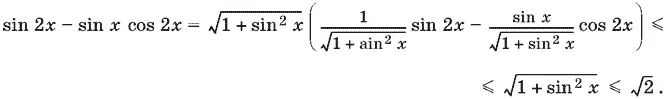
Так как левая часть рассматриваемого уравнения не превосходит √2, а правая часть равна 2, что больше √2, то данное уравнение не имеет корней.

Ответ.Нет решений.

13.45.Раскроем скобки и произведем перегруппировку членов:

(sin x cos x / 4+ cos x sin x / 4) − (2 sin² x + 2 cos² x ) + cos x = 0,

т. е.

sin 5 x / 4+ cos x = 2.

Так как sin 5 x / 4 ≤ 1 и cos x ≤ 1, то последнее уравнение равносильно системе

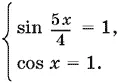
Решения второго уравнения x = 2π k подставим в первое уравнение. Выражение sin 5π x / 2перепишем в виде sin (2π k + 5π x / 2) = sin π k / 2, откуда следует, что sin 5 x / 4= 1 лишь при k = 4 n + 1.

Ответ. x = 2π(4 n + 1).

13.46.Введем новое неизвестное

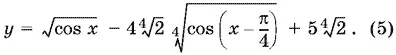
Получим квадратное уравнение относительно y :

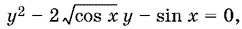
корни которого

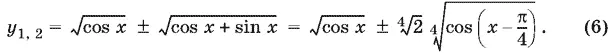
Обозначим 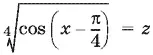и подставим в (6) вместо y его выражение (5) через x . Получим следствие исходного уравнения