Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Из первого условия cos² x = 1 находим x = π k . Так как cos 3π k ≠ 2 , то в этом случае решений мы не получаем.

На этом примере хорошо видно, что отказ от равносильных преобразований может позволить решить задачу проще и короче.

Ответ. π/ 2+ n π.

13.28.Данное уравнение равносильно системе

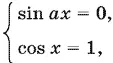
решая которую найдем ах = k π и x = 2 n π. Приравнивая значения неизвестного, найденные из каждого уравнения, получим

k π/ a = 2 n π, т. е. k / a = 2 n .

Это в том случае, если а ≠ 0. Но если а = 0, данное уравнение примет вид cos x = 1 и, следовательно, имеет бесконечное множество корней.

Итак, k = 2 nа .

Если а = p / q — рациональное число, то k = 2 np / q . Это значит, что при всех n , кратных q , мы будем получать корень данного уравнения x = 2 n π, т. е. уравнение имеет бесконечное множество корней.

Пусть теперь а — иррациональное число. Тогда при всех n , кроме n = 0, k не будет целым, а уравнение будет иметь единственное решение x = 0.

Ответ. а — иррациональное.

13.29.Так как второе уравнение легко приводится к виду

sin (2 x − y ) = 0,

то y = 2 x + π k . После подстановки этих значений y в первое уравнение получим

4 tg З х = 3 tg 4 x , или 4 (tg 4 x − tg З х ) = tg 4 x .

Используя простые преобразования, приходим к равносильным уравнениям:

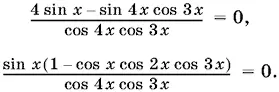
Выражение, стоящее в скобках, может обратиться в нуль лишь при условии, что cos x , cos 2 x , cos З х одновременно равны по абсолютной величине единице. Это означает, что непременно |cos x | = 1, т. е. корнями выражения, заключенного в скобки, могут быть лишь числа x = π n , являющиеся также и корнями множителя sin x . (Обратите внимание на то обстоятельство, что здесь нельзя написать x = π k , поскольку буква k уже занята в записи решения второго уравнения.)

Таким образом, все решения данной системы содержатся в системе чисел x = π n , y = π(2 n + k ), которую можно переписать так: x = π n , y = π k . Непосредственной подстановкой в исходную систему убеждаемся, что каждая пара из системы этих значений x и y является решением.

Ответ. x = π k , y = π n .

13.30.Преобразовав левую часть второго уравнения в разность косинусов, получим

cos (2y + x ) = О, откуда 2y = 2 − x + kn.

Приведем теперь первое уравнение системы к виду, удобному для логарифмирования:

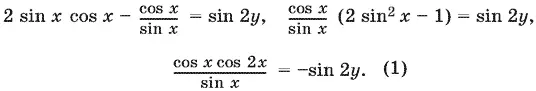
При подстановке в правую часть значения 2 y , полученного ранее, придется рассматривать случаи k = 2 p и k = 2 p + 1.

Если k = 2 p , то

2 y = π/ 2− x + 2 p π

и sin 2 y = cos x . Уравнение (1) преобразуется к виду

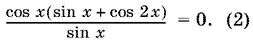
Если же k = 2 p + 1, то

2 y = π/ 2− x + π + 2 p π = 3π/ 2− x + 2 p π

и sin 2 y = −cos x . Уравнение (1) теперь примет вид

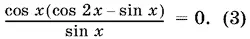
Поскольку значения x , при которых cos x = 0, удовлетворяют как уравнению (2), так и уравнению (3), то значениям x = (2 n + 1) π/ 2соответствуют все целые значения k. Поэтому

2 y = π/ 2− x + π k = π − π n + π k = π( k − n + 1).

Так как k − n + 1 принимает все целые значения для любого фиксированного k , то можно обозначить k − n + 1 = p . Получаем систему решений

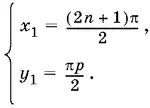
Остается приравнять нулю, выражения, стоящие в скобках в уравнениях (2) и (3).

Для уравнения (2) имеем

sin x + cos 2 x = 0, cos 2 x = cos ( x + π/ 2),

откуда x 2= (4 n + 1) π/ 2, x 3= (4 n − 1) π/ 6. Получаем еще две системы решений (здесь k = 2 p )

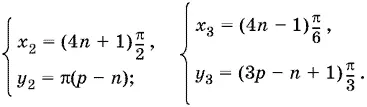
Для уравнения (3)

cos 2 x − sin x = 0, cos 2 x = cos ( π/ 2− x ),

откуда x 4= (4 n − 1) π/ 2, x 5= (4 n + 1) π/ 6. В этом случае k = 2 p + 1, и мы находим еще две системы решений

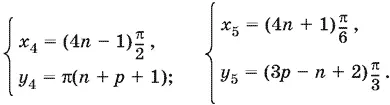
Нетрудно заметить, что вторая и четвертая системы решений содержатся в первой.

Проверка не нужна. (Докажите.)

Ответ.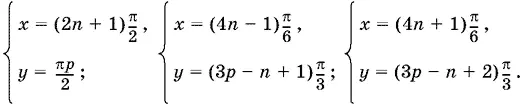

13.31.Перепишем систему в виде

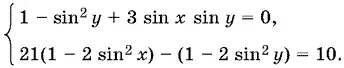
Введем обозначения: sin x = u , sin y = v . Получим систему

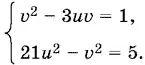
Воспользуемся заменой v = ut :

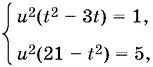
откуда

5( t ² − 3 t ) = 21 − t ²,

т. е.

2 t ² − 5 t − 7 = 0, t 1= 7/ 2, t 2= −1.

Если t = 7/ 2, то из первого уравнения последней системы мы получим

u ² = 4/ 7; u ± 2/ √7; v = ut = ± 2/ √7 7/ 2= ±√7,

что невозможно, так как v = sin y .

Если же t = −1, то u ² = ¼, u = ±½.

Приходим к совокупности двух систем

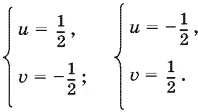
Ответ.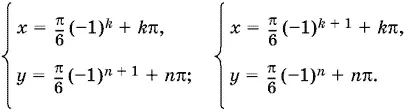

13.32.Второе уравнение можно преобразовать так:

sin y + sin (2 x − y ) = sin y ,

т. е. sin (2 x − y ) = 0, откуда y = 2 x + n π. Подставим в первое уравнение системы

4 tg 3 x = 3 tg 4 x .

При условии что cos 3 x ≠ 0 и cos 4 x ≠ 0, это уравнение равносильно такому:

4 sin 3 x cos 4 x − 3 sin 4 x cos 3 x = 0,

или

sin 3 x cos 4 x − 3 (sin 4 x cos 3 x − sin 3 x cos 4 x ) = 0,

sin 3 x cos 4 x − 3 sin x = 0.

Так как sin 3 x cos 4 x = ½(sin 7 х − sin x ), то придем к уравнению

7 sin x = sin 7 x .

По индукции можно доказать, что