Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Если tg x ≠ 0, то 2 − 2 tg² x = 1, tg x = ± 1/ √2. Так как cos 3 x и cos 4 x не обращаются при этом в нуль, то можно написать ответ.

Ответ. n π; n π ± arctg 1/ √2.

13.9.Уравнение можно переписать так:

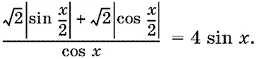
Поскольку 0 < x < 2π, то 0 < x / 2< π и sin x / 2> 0. Однако cos x / 2в этом интервале меняет знак, и нам придется разбить интервал на два: 0 < x ≤ π и π < x < 2π.

Если 0 < x ≤ π, получим уравнение

√2/ 2sin x / 2+ √2/ 2cos x / 2= sin 2 x ,

y которого может появиться лишь один посторонний корень при cos x = 0. Перепишем последнее уравнение так:

sin ( x / 2+ π/ 4) = sin 2 x ,

и найдем его корни из интервала 0 < x ≤ π: x 1= π/ 6, x 2= 3π/ 10. Если π < x < 2π, придем к уравнению

√2/ 2sin x / 2− √2/ 2cos x / 2= sin 2 x или sin ( x / 2− π/ 4) = sin 2 x ,

которое даст нам еще два корня: x 3= 7π/ 6, x 4= 13/ 10π. Очевидно, что для полученных углов cos x ≠ 0.

Ответ. π/ 6; 3π/ 10; 7π/ 6; 13π/ 10.

13.10.Перенеся sin α в левую часть, запишем уравнение в виде

2 sin x / 2cos x − 2α/ 2 = 2 sin x / 2cos x / 2,

или

sin x / 2(cos x − 2α/ 2 − cos x / 2) = 0.

Если sin x / 2 = 0, то x = 2 n π при любом α. Если cos x − 2α/ 2 = cos x / 2, то либо x − 2α/ 2+ x / 2 = 2 n π, откуда x = 2 n π + α, либо x − 2α/ 2− x / 2 = 2 n π, откуда α = 2 n π.

Ответ.При любом α: 2 n π, 2 n π + α; при α = 2 n π: x − любое.

13.11.Уравнение равносильно совокупности двух уравнений

cos 2 x = sin² x − a , cos 2 x = a − sin² x .

Понизим степень в правой части каждого уравнения и найдем

cos 2 x = 1 − 2 a / 3, cos 2 x = 2 a − 1.

Первое уравнение имеет решение, если

−1 ≤ 1 − 2 a / 3 ≤ 1, т. е. −1 ≤ a ≤ 2.

Второе уравнение имеет решение, если −1 ≤ 2 a − 1 ≤ 1, т. е. 0 ≤ a ≤ 1. Данное в условии уравнение при −1 ≤ a ≤ 2 имеет решения

x = π n ± ½ arccos 1 − 2 a / 3,

а при 0 ≤ a ≤ 1 решения

x = π n ± ½ arccos (1 − 2 a ).

Так как

0 ≤ ½ arccos 1 − 2 a / 3 ≤ π/ 4и 0 ≤ ½ arccos (1 − 2 a ) ≤ π/ 2,

то легко найти решения нашего уравнения, которые попадут в интервал 0 ≤ x ≤ 2π.

Ответ.½ arccos 1 − 2 a / 3; π ± ½ arccos 1 − 2 a / 3; 2π − ½ arccos 1 − 2 a / 3(существуют при −1 ≤ a ≤ 2);

½ arccos (1 − 2 a ); π ± ½ arccos (1 − 2 a ); 2π − ½ arccos (1 − 2 a ) (существуют при 0 ≤ a ≤ 1).

13.12.Преобразуем подкоренное выражение следующим образом:

sec² (17 + 8 sin x − 16 cos² x ) = sec² x (1 + 8 sin x + 16 sin² x ) = sec² x (1 + 4 sin x )².

Данное уравнение принимает вид

|1 + 4 sin x |/ |cos x |= 2 tg x (1 + 4 sin x ).

Если 1 + 4 sin x = 0, то x = n π + (−1) n + 1arcsin ¼. Это — корни нашего уравнения, так как cos x ≠ 0 и tg x существует.

Если 1 + 4 sin x ≠ 0, то придется рассмотреть два случая, зависящих от знака этого выражения.

Пусть 1 + 4 sin x > 0, т. е. sin x > −¼. Тогда придем к уравнению

1/ |cos x |= 2 tg x , или 2 tg x |cos x | = 1,

которое равносильно совокупности систем

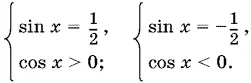
Вторая система не имеет решений при sin x > −¼. Решение первой: x = π/ 6+ 2 n π.

Пусть, наконец, 1 + 4 sin x < 0, т. е. sin x < −¼. Уравнение

2 tg x |cos x | = −1,

к которому мы приходим в этом случае, равносильно такой совокупности систем:

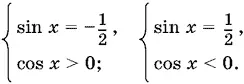
Вторая система не имеет решений при sin x < −¼, а первая дает нам x = − π/ 6+ 2 n π.

Ответ. n π + (−1) n + 1arcsin ¼; ± π/ 6+ 2 n π.

13.13.Поскольку tg x + sin x = tg x (1 + cos x ) = 2 tg x cos² x / 2, а tg x − sin x = 2 tg x sin² x / 2, данное уравнение можно записать в виде

√2 tg ½ x (|cos x / 2| + |sin x / 2| − √2 cos x ) = 0.

Первые решения получим при tg x = 0; x = k π. Остальные решения нам доставят корни уравнения

|cos x / 2| + |sin x / 2| = √2 cos x ,

при которых tg x > 0 (случай tg x = 0 уже исследован). Решим вначале последнее уравнение, а затем исключим те решения, которые не удовлетворяют неравенству tg x > 0. Возведем это уравнение в квадрат и, чтобы не нарушить равносильности, добавим ограничение cos x ≥ 0. Получим систему

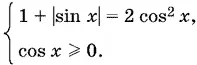
Так как одновременно tg x > 0 и cos x > 0, то sin x > 0. Поэтому

|sin x | = sin x .

Приходим к уравнению

2sin² x + sin x − 1 = 0.

Решая его, найдем

|sin x | = −1 ± 3/ 4.

Так как |sin x | ≥ 0, то остается решить уравнение

|sin x | = ½,

корнями которого будут числа

x = π/ 6+ 2π k , x = 5π/ 6+ 2π k .

Остается вспомнить, что tg x > 0.

Ответ. k π, π/ 6+ 2 k π.

13.14.При замене 1/ sin 4 x на 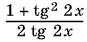можно ожидать потери корней, при которых tg 2 x не существует, или, что то же самое, cos 2 x = 0. Однако при cos 2 x = 0 обращается в нуль и sin 4 x , т. е. потери корней не произойдет.

Так как в левую часть уравнения

ctg 2 x + 3 tg 3 x = 2 tg x + (1 + tg² 2 x ) 1/ tg 2 x

входит ctg 2 x , то, заменив 1/ tg 2 x на ctg 2 x и раскрыв скобки, мы уничтожим в правой и левой частях ctg 2 x . Замена 1/ tg 2 x = ctg 2 x грозит лишь приобретением корней, при которых tg 2 x не существует, т. е. безопасна, так как tg 2 x остается в уравнении. Когда происходит уничтожение одинаковых слагаемых ctg 2 x , то нужно добавить к уравнению

3 tg 3 x = 2 tg x + tg 2 x ,

условие

ctg 2 x существует.

Мы воспользовались попутно неабсолютным тождеством tg 2 x ctg 2 x = 1, которое не приводит к приобретению посторонних корней, так как tg 2 x и ctg 2 x остались в системе.

Преобразуем уравнение следующим образом:

2(tg 3 x − tg x ) + tg 3 x − tg 2 x = 0,

т. е.

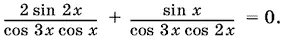
Теперь систему можно переписать так:

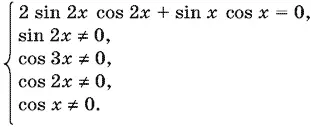
Так как sin 2 x ≠ 0, то на него можно сократить. Получим уравнение

cos 2 x = −¼,

откуда x = ±arccos(−¼) + k π. Поскольку при этих x все ограничения выполняются, найденные значения x являются решениями данного уравнения.