Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Ответ.(1, −1).
11.25.Первое уравнение системы можно переписать в виде
log 8( y − x )³ = log 8(3 y − 5 х ).
Следствием данной системы является система
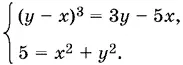
Перемножив входящие в нее уравнения, получим однородное уравнение относительно x и y :
5( y − x )³ = (3 y − 5 х )( х ² + y ²).
Если x ≠ 0, то разделим последнее уравнение почленно на x ³ и обозначим y / x = u . Получим уравнение относительно u :
u³ − 5 u ² + 6 u = 0,
которое имеет корни: u 1= 0, u 2= 2, u 3= 3.
Если u = 0, то y = 0, а из второго уравнения исходной системы x = ±√5.
При подстановке в первое уравнение исходной системы x = −√5 и y = 0 это уравнение удовлетворяется, а при x = √5 и y = 0 уравнение не удовлетворяется. Если u = 3, то y = 3 x , а потому x ² = ½, откуда
x =± 1/ √2, y = ± 3/ √2
( x и y в силу равенства y = 3 x имеют одинаковые знаки). Подстановкой в первое уравнение убеждаемся, что решением системы будут
x = 1/ √2, y = 3/ √2.
Если u = 2, то y = 2 x . Из двух систем значений (−1, −2), (1, 2) первому уравнению удовлетворяет только вторая.
Осталось рассмотреть случай x = 0. Он не дает новых решений, так как система превращается в два несовместных уравнения.
Ответ.(−√5, 0); ( 1/ √2, 3/ √2); (1, 2).
11.26. Способ 1.Из второго уравнения
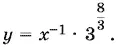
Подставляем в первое:
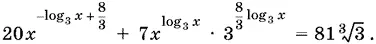
Так как
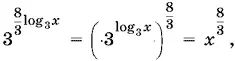
то получим уравнение
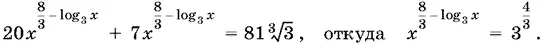
Прологарифмируем по основанию 3:
3log 3² x − 8log 3 x + 4 = 0,
откуда x 1= 3 ⅔, x 2= 9.
Находим соответствующие y и делаем проверку.
Способ 2.Применим равенство  (оно доказывается с помощью логарифмирования) к первому уравнению. Получим
(оно доказывается с помощью логарифмирования) к первому уравнению. Получим
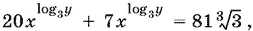
т. е. 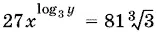 или
или 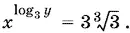
Прологарифмировав по основанию 3, решим полученное уравнение совместно со вторым уравнением системы:
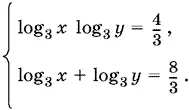
Ответ. 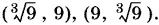
11.27.Так как x и y одного знака (это следует из второго уравнения) и x + y > 0 (из первого), то x и y положительны, причем либо x , либо y обязательно больше 1 (так как xy = 3). Следовательно, x + y > 1 и данная система может быть переписана так:
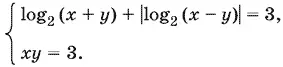
Если 0 < x − y < 1, то получим систему
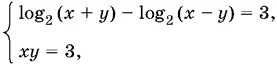
следствием которой является система
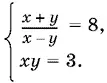
Из первого уравнения получим 7 x = 9 y . Подставляя сюда y = 3/ x , найдем x ² = 27/ 7, откуда
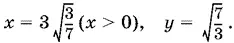
Убеждаемся, что при этих значениях x и y неравенство 0 < x − y < 1 выполняется.
Если x − y > 1, то получим систему
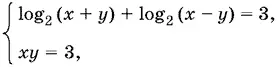
следствием которой является система
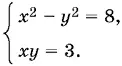
Подставляя в первое уравнение y = 3/ x , получим уравнение
x 4− 8 x ² − 9 = 0.
Так как x ² ≠ −1, то остается x ² = 9, откуда x = 3, а y = 1. (Ограничение x − y > 1 удовлетворяется.)
Равносильность могла быть нарушена только при потенцировании; поэтому достаточно проверить, что x − y > 0, что уже сделано.
Ответ. 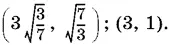
11.28.Прологарифмируем и обозначим log 2 x = u , log 2( y + 1) = u :
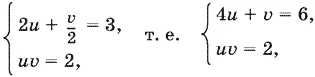
откуда
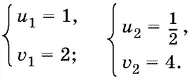
Находим соответствующие x и y ; проверка не обязательна, так как равносильность не была нарушена.
Ответ.(√2, 15); (2, 3).
11.29.Так как log a ² x = ½ log ax (обратите внимание на то, почему мы не пишем здесь log | a | x ), а log √ b √ y = log by , то систему можно переписать следующим образом:
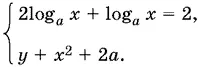
Это — следствие первоначальной системы; если же добавить условия y > 0, b > 0, b ≠ 1, то получим равносильную систему.
Из первого уравнения
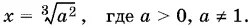
Подставляем во второе и находим
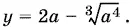
Условие 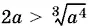 , т. е. 8 а ³ > а 4, приводит к дополнительному ограничению на а : а < 8.
, т. е. 8 а ³ > а 4, приводит к дополнительному ограничению на а : а < 8.
Ответ.При 0 < а < 1, 1 < а < 8 и при b > 0, b ≠ 1 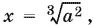
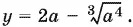
Интервал:
Закладка:










