Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. x ∈ (−5; +∞).

10.51.Ясно, что подставлять интересующие нас значения x в данное неравенство и проверять, удовлетворяется ли это, не нужно. Проще это неравенство решить. Так как lg 5 ≠ ½, то |0,5 − lg 5| > 0, т. е.

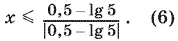
Любое число а ^ 0 можно записать в виде а = | а | sign а , где

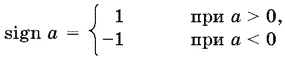
— функция, соответствующая знаку числа а . Поэтому из (6) получаем

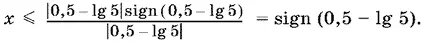
Определим теперь знак выражения

0,5 − lg 5 = lg √10 − lg 5 = lg √10/ 5< lg 4/ 5< lg 1 = 0.

Следовательно, sign (0,5 − lg 5) = −1, т. е. решением неравенства (6) будут значения x ≤ −1.

Ответ.−4, −1.

10.52.Так как (√5 + 2)(√5 − 2) = 1, то данное неравенство можно преобразовать к виду

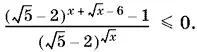
(7)

Знаменатель всегда положителен, если x ≥ 0. Требование x ≥ 0 сохраняется, если существует числитель. Поэтому (7) равносильно неравенству

(√5 − 2) x + √ x − 6 ≤ 1. (8)

Поскольку 0 < √5 − 2 < 1, то (8) равносильно неравенству

x + √ x − 6 ≥ 0. (9)

Трехчлен y ² + y − 6 (где y = √ x ) имеет корни −3 и 2. Поэтому решением неравенства

y ² + y − 6 ≥ 0

будет совокупность значений y ≤ −3, y ≥ 2. У неравенства √ x ≤ −3 решений нет. Остается √ x ≥ 2, т. е. x ≥ 4.

Ответ.[4, +∞).

10.53.Обозначим log 2 x = y и запишем неравенство в виде

1 + y ² ≤ | y | (4 x − x ² − 2),

или

1 + y ² ≤ | y | [−( x ² − 4 x + 4) + 2],

т. е.

1 − 2| y | + | y ²| ≤ | y |(− x ² + 4 x − 4).

Итак,

(1 − | y |)² ≤ −| y |( x − 2)².

Неравенство удовлетворяется только в том случае, если обе его части равны нулю. Это может быть только при | y | = 1, тогда ( x − 2)² ≤ 0, т. е. x = 2.

Ответ.2.

11.1.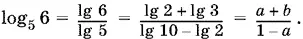

11.2.Так как 1225 = 35², то

lg 122,5 = lg 35² − lg 10 = 2(lg 5 + lg 7) − 1 = 2( а + b ) − 1.

11.3.Перепишем уравнение в виде

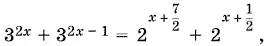
т. е. после того как вынесем 3 2 x − 1и 2 x + ½ за скобки,

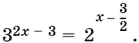
Из последнего уравнения следует, что

3 2 x − 3= (√2) 2 x − 3,

т. е. ( 3/ √2) 2 x − 3= 1, откуда 2x − 3 = 0.

Ответ. x = 3/ 2.

11.4.Обозначив 3 −| x − 2|= y , придем к квадратному уравнению

y ² − 4 y − а = 0,

корни которого

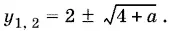
Первый корень 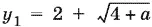приходится отбросить, так как −| x − 2| ≤ 0 и 3 −| x − 2| ≤ 1, а 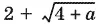не может стать меньше двух.

Исследуем второй корень:

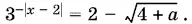
Чтобы это уравнение имело решение, необходимо выполнение трех условий, которые сведены в систему неравенств:

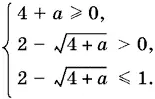
Решая эту систему, найдем −3 ≤ а < 0.

Ответ.При −3 ≤ а < 0 два решения:

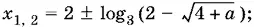
при остальных а решений нет.

11.5.Решая квадратное уравнение относительно 12 | x |, найдем

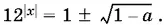
Первое ограничение: 1 − а ≥ 0, т. е. а ≤ 1. Кроме того, 12 | x |не может стать меньше единицы. Если перед корнем выбран знак плюс, то последнее требование выполняется, если же взят знак минус, то 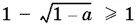лишь при а = 1. Это значение а можно учесть при рассмотрении уравнения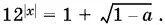

Ответ. 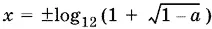при а ≤ 1; при остальных а решений нет.

11.6.Уравнение можно записать так:

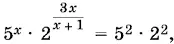
или

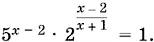
Прологарифмируем по основанию 10

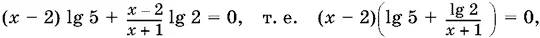
откуда x 1= 2, x 2= − 1/ lg 5.

Ответ.2, − 1/ lg 5.

11.7.Так как (2 + √3)(2 − √3) = 1, то 2 + √3 и 2 − √3 — взаимно обратные числа. Обозначим

(2 + √3) x ² − 2 x = y .

Тогда данное уравнение можно записать так:

y + 1/ y = 101/ 10

(мы разделили обе части уравнения на 2 + √3).

Решая это уравнение, найдем

y 1= 1/ 10, y 2= 10.

Покажем, что первый корень, который приводит к уравнению

(2 + √3) x ² − 2 x = 1/ 10,

посторонний.

Так как 2 + √3 > 1, то x ² − 2 x < 0. Выражение x ² − 2 x достигает своего минимума в точке x = 1. Этот минимум равен −1. Поскольку 2+ √3 < 4, то в левой части последнего уравнения стоит число, большее ¼, а следовательно, ни при каких x не равное 1/ 10.

Остается решить уравнение

(2 + √3) x ² − 2 x = 10.

Прологарифмируем его по основанию 2 + √3:

x ² − 2 x − log 2 + √310 = 0.

Ответ.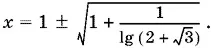

11.8.Перепишем уравнение так:

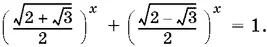
Сразу же видно, что x = 2 — корень уравнения. Покажем, что других корней нет.