Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

где n — целое. Из условия x < 0 находим

x = 10 n − 2/ 5 − 5 n < 0,

откуда n < 1/ 5, n > 1, или n ≠ 1. Мы получили бесконечное множество значений x . Чтобы выбрать из них подходящие, разберем два случая, в зависимости от того, четное или нечетное число n. Когда n = 2 k , данное неравенство можно переписать в виде | x | 2 k < 1, т. е. (| x | − 1) k < 0. Поскольку x < 0, то получаем ( x + 1) k > 0. Так как x = 20 k − 2/ 5 − 10 k , то

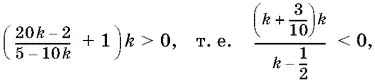
откуда k < − 3/ 10, 0 < k < ½. Так как k — целое, то k = −1, −2, −3, ... . Получаем серию решений первоначального неравенства: x = 20 k − 2/ 5 − 10 k , k = −1, −2, −3, ... .

Пусть теперь n = 2 k + 1. Тогда x = 10(2 k + 1) − 2/ 5 − 5(2 k + 1)= − 10 k + 4/ 5 k . Так как x < 0, то исходное неравенство при этих значениях n удовлетворяется, если n ≠ 1, т. е. k ≠ 0.

Ответ.0 ≤ x < 1, x = 20 k − 2/ 5 − 10 k , k = −1, −2, −3, ...; x = − 10 k + 4/ 5 k , k = ±1, ±2, ±3, ... .

10.33.Данное неравенство эквивалентно неравенству

0 ≤ log 2 3 − 2 x / 1 − x < 1.

(Ограничение слева обеспечивает неотрицательность числа, стоявшего под знаком квадратного корня.)

Поскольку 0 = log 21, 1 = log 22 и основание логарифмов больше единицы, последнее неравенство можно записать так:

1 ≤ 3 − 2 x / 1 − x < 2.

Требование положительности числа 3 − 2 x / 1 − x , которое могло быть нарушено при таком преобразовании, выполняется здесь автоматически.

Поскольку неравенство 1 ≤ y < 2 эквивалентно неравенству y − 1/ y − 2≤ 0, получаем

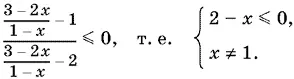
Ответ. x ≥ 2.

10.34.Данное неравенство равносильно системе

0 < | x − 1/ 2 x + 1| < 1.

Тем самым мы обеспечили положительность числа, стоявшего в условии под знаком логарифма. Левое неравенство можно заменить условием x ≠ 1. Тогда получим систему

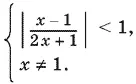
Эту систему можно преобразовать так:

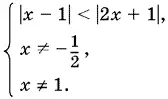
Входящее в эту систему неравенство можно возвести в квадрат, не нарушая его равносильности:

( x − 1)² < (2 x + 1)²,

т. е. 3 x ² + 6 х > 0, откуда x < −2, x > 0. Итак,

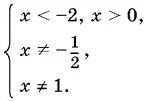
Ответ. x < −2, 0 < x < 1, x > 1.

10.35.Приведем все логарифмы, участвующие в неравенстве, к основанию 5:

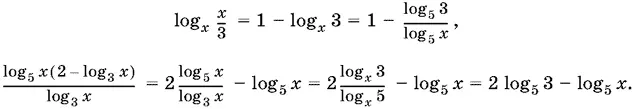
Последнее из преобразований правой части неравенства требует, вообще говоря, ограничения x ≠ 1. Однако это значение неизвестного оказывается «запретным», поскольку в левой части остается выражение, содержащее log 5 x в знаменателе. Получаем равносильное неравенство

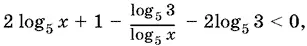
которое преобразуется к виду

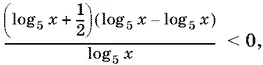
допускающему применение метода интервалов. Итак,

log 5 x < −½, 0 < log 5 x < log 53.

Ответ.0 < x < 1/ √5, 1 < x < 3.

10.36.Так как log ½ N = −log 2 N , то данное неравенство перепишем в виде

log 2(2 x − 1)log 2(2 x + 1− 2) < 2.

Преобразуем второй сомножитель:

log 2(2 x + 1− 2) = log 2[2(2 x − 1)] = 1 + log 2(2 x − 1).

Обозначив log 2(2 x − 1) = y , получим квадратное неравенство

y ( y + 1) < 2, или y ² + y − 2 < 0,

решения которого лежат в интервале

−2 < y < 1.

Вспоминая, чему равен y , получим

−2 < log 2(2 x − 1) < 1,

¼ < 2 x − 1 < 2, 5/ 4< 2 x < 3.

Ответ.log 25 − 2 < x < log 23.

10.37.Преобразуем левую часть неравенства:

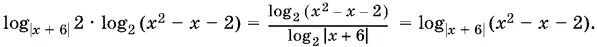
Неравенство

log | x + 6|( х ² − x − 2) ≥ 1

равносильно совокупности двух систем

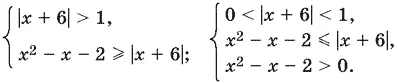
Второе неравенство первой системы равносильно совокупности систем решая которые найдем

x ≤ −2, x ≥ 4.

Таким образом, первая система может быть приведена к виду

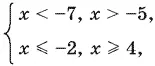
и ее решениями будут интервалы:

x < −7, −5 < x ≤ −2, x ≥ 4.

Решая второе неравенство второй системы, получим −2 ≤ x ≤ 4, а третье неравенство имеет решения x < −1, x > 2. Следовательно, система принимает вид

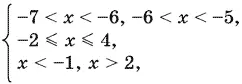
т. е. не имеет решений.

Ответ. x < −7, −5 < x ≤ −2, x ≥ 4.

10.38.Обозначим log а x = y. Неравенство примет вид

1 + y ²/ 1 + y > 1.

Так как 1 + y ² > 0, то и 1 + y > 0. Поэтому данное неравенство равносильно системе

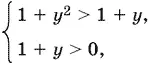
т. е.

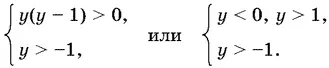
Получаем два интервала решений:

−1 < y < 0, y > 1.

Так как y = log а x , то нужно рассмотреть два случая.

Во−первых, если а > 1, то log а x − функция возрастающая и мы получим два интервала решений:

1/ a < x < 1, x > а .

Если же 0 < а < 1, то получим другие два интервала решений:

1 < x < 1/ a , 0 < x < а .

Ответ.При а > 1: 1/ a < x < 1, x > а; при 0 < а < 1: 0 < x < а, 1 < x < 1/ a .

10.39.Перейдем к основанию k :

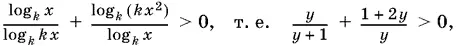
где y = log k x . Последнее неравенство можно переписать так:

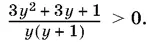
Выражение, стоящее в числителе, всегда положительно. Поэтому решением неравенства будут два интервала: