Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

u ² + ( x − х ³) u + x ² = 0.

По условию числа x и z действительные. Следовательно, дискриминант

D = ( x − x ³)² − 4 x ² = x ²(1 − x ²)² − 4 x ² = x ²[(1 − x ²)² − 4]

должен быть неотрицательным.

Так как по условию x ≠ 0, то

(1 − x ²)² ≥ 4.

Это неравенство может выполняться, если либо 1 − x ² ≤ −2, либо 1 − x ² ≥ 2. Второе неравенство не имеет решений, а из первого получаем x ² ≥ 3, что и требовалось доказать.

10.13.Перепишем данные уравнения в виде откуда

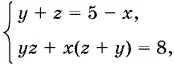
yz = 8 − x (5 − x ).

Числа y и z будут корнями уравнения

u ² − (5 − x ) u + x ² − 5 х + 8 = 0.

Так как y и z должны быть действительными числами, то дискриминант этого уравнения не может стать отрицательным ни при каких значениях x :

(5 − x )² − 4( х ² − 5 х + 8) ≥ 0, т. е. −3 x ² + 10 x − 7 ≥ 0,

откуда

1 ≤ x ≤ 7/ 3.

Так как уравнения, которым удовлетворяют x , y и z , симметричны, то аналогичные ограничения получим для y и z :

1 ≤ y ≤ 7/ 3, 1 ≤ z ≤ 7/ 3,

что и требовалось доказать.

10.14.Дискриминант квадратного трехчлена равен 1 − 4 а . Если а < ¼, то дискриминант положителен и уравнение ax ² + x + 1 = 0 имеет два различных корня:

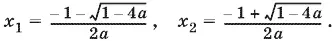
Когда а > 0, т. е. 0 < а < ¼, то получим решения неравенства:

x < x 1, x > x 2.

Когда а < 0, то легко проверить, что x 2< x 1. Поэтому решения запишутся в виде

x 2< x < x 1.

Дискриминант отрицателен, когда а > ¼, а следовательно, а > 0. Неравенство удовлетворяется при всех x .

Если а = ¼, то решения неравенства запишутся в виде x ≠ −2.

10.15.Условия задачи выполняются тогда и только тогда, когда интервал 1 < x < 2 будет расположен между корнями параболы, т. е. если

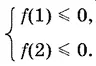
Подставляя значения 1 и 2 в данный трехчлен, получим систему двух квадратных неравенств

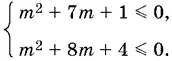
Решая первое неравенство, найдем

−7 − 3√5/ 2≤ m ≤ −7 + 3√5/ 2,

а решая второе, получим

−4 − 2√3 ≤ m ≤ −4 + 2√3.

Ответ.−½(7 + 3√5) ≤ m ≤ −4 + 2√3.

10.16.Пусть x 1и x 2— корни данного трехчлена. Тогда

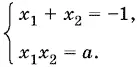
Если корни x 1и x 2действительны, то из первой формулы следует, что они не могут быть оба положительными. Если оба корня отрицательны, то из второй формулы находим а > 0, а следовательно, корни x 1и x 2меньше а . Если а = 0, то один из корней равен −1, и условие задачи снова не выполняется. Таким образом, а < 0. При а < 0 дискриминант 1 − 4 a положителен и оба корня действительные. Потребуем, чтобы меньший из них был больше а , т. е.

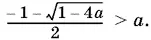
Это неравенство эквивалентно такому:

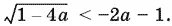
Возведя обе части неравенства в квадрат, мы должны позаботиться о сохранении связей, которые неявно присутствуют в этом неравенстве:

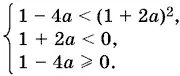
Последнее неравенство выполняется, так как мы установили, что а < 0. Первые два преобразуются к виду

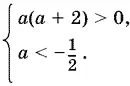
Ответ. а < −2.

10.17.Так как k ≠ 0, то ветви параболы направлены вверх. Внутри интервала от −1 до +1 парабола имеет только один корень тогда и только тогда, когда на концах этого интервала трехчлен имеет разные знаки, т. е.

( k ² − k − 2)( k ³ + k − 2) < 0.

Разлагая каждый из трехчленов на множители, получим

( k − 2)( k + 1)( k + 2)( k − 1) < 0.

Ответ.−2 < k < −1; 1 < k < 2.

10.18.Условие, что ветви параболы направлены вверх, означает, что m > 0. Если парабола не пересекает ось Ox , то получаем систему

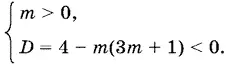
Если же данный квадратный трехчлен имеет действительные корни, то больший корень не должен быть положительным:

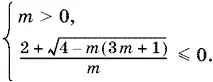
Второе неравенство второй системы (а следовательно, и вся система) не имеет решений при m > 0, так как числитель и знаменатель оказываются положительными.

Решая второе неравенство первой системы, найдем

m < − 4/ 3, m > 1.

Принимая во внимание первое неравенство, находим решение системы: m > 1.

Пусть теперь m = 0. Правая часть данного неравенства принимает вид −4 x + 1 > 0, т. е. x < ¼, и неравенство удовлетворяется не при всех положительных x .

Ответ. m > 1.

10.19.Неравенство равносильно совокупности двух систем

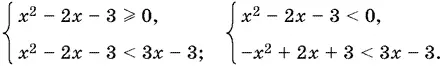
Решая каждое из четырех неравенств, придем к новой совокупности двух систем:

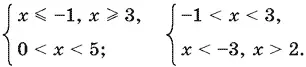
Итак, 3 ≤ x < 5, 2 < x < 3.

Ответ.2 < x < 5.

10.20.Неравенство можно переписать в виде

( x − 3)² > ( x + 2)²,

откуда после раскрытия скобок и приведения подобных получим линейное неравенство.

Ответ. x < ½.

10.21.При x > 0 неравенство можно переписать в виде

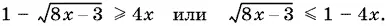
Последнее неравенство равносильно системе

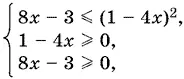
которая несовместна, так как несовместны два последних неравенства.

При x < 0 входящее в данное неравенство выражение 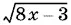не существует.