Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

одно решение x 1при а < −2;

решений нет при −2 ≤ а < − 4/ 3;

одно решение x 1= x 2при а = − 4/ 3;

два решения x 1, x 2при − 4/ 3< а < −½;

два решения x 1, x 2= x 3при а = −½;

два решения x 2, x 3при −½ < а < − 4/ 9;

три решения x 1, x 3, x 4= x 5при а = − 4/ 9;

четыре решения x 1, x 3, x 4, x 5при − 4/ 9< а < −¼;

три решения x 1, x 3= x 4, x 5при а = −¼;

два решения x 1, x 5при −¼ < а < 2;

одно решение x 1при а ≥ 2.

Замечание: при а = −2 решений нет, а при а = 2 есть единственное решение x 1, которое при а = 2 существует.

9.36.После возведения в квадрат и приведения подобных можно утверждать, что уравнение равносильно системе

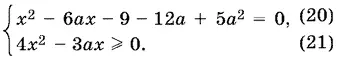
Дискриминант уравнения (20) равен 4a² + 12a + 9 = (2a + 3)². Он неотрицателен. Уравнение имеет один корень x = 3a при а = − 3/ 2и два корня x 1,2= 3a ± |2a + 3| при остальных а.

Если а = − 3/ 2, то x = − 9/ 2. При этих значениях а и x неравенство (21) удовлетворяется.

Пусть а < − 3/ 2. Тогда |2a + 3|= −2a − 3, т. е. x 1= 5 а + 3, x 2= а − 3. Для каждого из этих корней решим неравенство (21) и учтем ограничение а < − 3/ 2. Пусть сначала x 1= 5 а + 3, тогда:

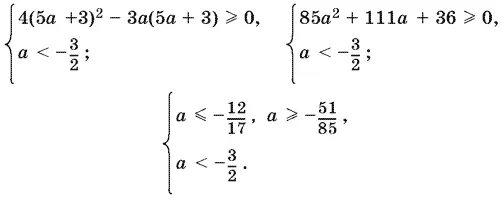
Решением последней системы будет а < − 3/ 2, т. е. корень x 1= 5 а + 3 существует при всех а < − 3/ 2.

Пусть теперь x 2= а − 3, тогда:

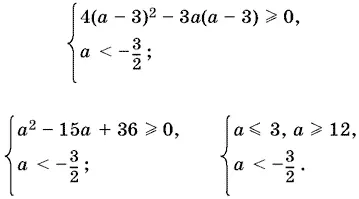
Итак, корень x 2= а − 3 существует при всех а < − 3/ 2.

Таким образом, при а < − 3/ 2исходное уравнение имеет два корня x 1= 5 а + 3 и x 2= а − 3.

Аналогично исследуется случай а < − 3/ 2. При этом |2a + 3| = 2a + 3 и соответственно x 1= 3a − (2a + 3); x 2= 3a + (2a + 3) = 5 а + 3. Подставляем эти значения в (21). Для x 1= а − 3 получим:

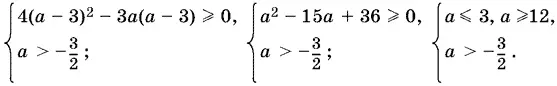
Аналогично для x 2= 5 а + 3 имеем:

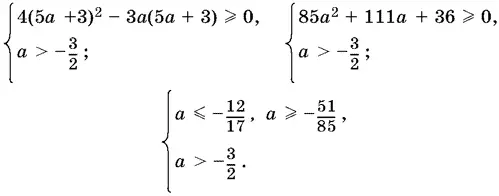
Итак, x 1= а − 3 будет корнем исходного уравнения, когда

− 3/ 2< а ≤ 3 и а ≥ 12.

x 2= 5 а + 3 будет корнем, когда − 3/ 2< а ≤ − 12/ 17; а ≥ − 51/ 85.

Обобщим результаты на числовой оси а (рис. P.9.36).

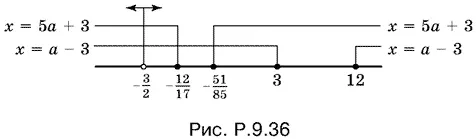
Ответ.При a ∈ (−∞, − 3/ 2) ∪ (− 3/ 2, − 12/ 17) ∪ (− 51/ 85, 3) ∪ [12, +∞) уравнение имеет два корня: x 1= 5 а + 3, x 2= а − 3. При а = −3 имеет один корень x = 3a = − 9/ 2. При а ∈ (− 12/ 17, − 51/ 85) уравнение имеет один корень x = а − 3, а при а ∈ (3, 12) — один корень x = 5 а + 3.

9.37.Уравнение можно записать в виде

x ( 5 x / 5 x ² − 7 x + 6+ 2 x / 5 x ² − x + 6− 1) = 0.

При x = 0 множитель в скобках существует и равен −1. Поэтому x = 0 — корень данного уравнения. Другие корни должны быть корнями уравнения

5 x / 5 x ² − 7 x + 6+ 2 x / 5 x ² − x + 6 = 1. (22)

В знаменателях стоят симметрические многочлены. Значение x = 0 не является корнем (22) и выражение (22) не теряет при этом значении смысла. Поэтому разделим числители и знаменатели каждой дроби на x :

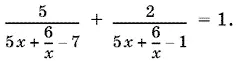
Проведем замену

t = 5 х + 6/ x . (23)

Тогда

5/ t − 7+ 2/ t − 1= 1. (24)

Дальше решение стандартно. Уравнение (24) имеет корни t 1= 13 и t 2= 2. Подставляя их в (23), найдем для t 1значения x 2= 2, x 3= 3/ 5. Для t 2решений нет.

Ответ.0; 2; 3/ 5.

9.38.Пусть x + y = u , xy = v . Тогда получим

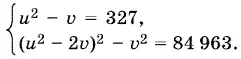
Во второе уравнение подставим u ² = v + 327:

(327 − v )² − v ² = 84 693,

или

327² − 2 · 327 v = 84 963.

Так как 84 693 = 327 · 259, то сократим уравнение на 327 и найдем v = 34, u ² = 361.

Остается решить две системы:

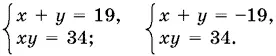
Ответ.(2, 17), (17, 2), (−2, −17), (−17, −2).

Ответык упражнениям на с. 59, 62 и 63.

1.Получим совокупность неравенств, имеющую те же самые решения.

2.Получим систему неравенств, не имеющую решений.

3. Ответ.−1 < x ≤ 1, 5 < x ≤ 7, x > 8.

4.Вначале нужно переписать неравенство в виде

( x − 5/ 2)( zx − 3)( x − 4)² ≤ 0.

Последний множитель показывает, что точка 4 обязательно должна принадлежать множеству решений, этим его влияние ограничивается.

Ответ. 5/ 2 ≤ x ≤ 3, x = 4.

5.Поскольку неравенство строгое, то множители, стоящие в знаменателе, и множители, стоящие в числителе, играют одинаковую роль. Данное неравенство равносильно такому:

( x + 3)²( x + 1)( x − 2)( x − 4)²( x − 5) < 0.

Достаточно решить неравенство

( x + 1)( x − 2)( x − 5) < 0

и исключить, если они попали в множество решений, точки x = −3, x = 4.

Ответ. x < −3, −3 < x < −1, 2 < x < 4, 4 < x < 5.

6.0 ≤ ax ² + bх + с < 9.

7. ax ² + bх + с ≥ 9; здесь не нужно заботиться о знаке подкоренного выражения, так как после возведения в квадрат получаем неравенство, из которого следует, что это выражение положительно.

8.

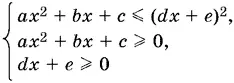
(см. пример 4 на с. 62).

9.Нужно разобрать два случая в зависимости от знака правой части: если правая часть отрицательна, то неравенство удовлетворяется при всех x , при которых левая часть существует; если правая часть неотрицательна, то обе части неравенства нужно возвести в квадрат (подкоренное выражение при этом не может стать отрицательным):

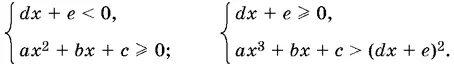
10.1.Обозначим а = 1 + k . Тогда из условия а + b = 2 получим b = 1 − k. Вычислим а 4+ b 4:

а 4+ b 4= (1 + k ) 4+ (1 − k ) 4= 2 k 4+ 12 k ² + 2 = 2( k 4+ 6 k ² + 1) ≥ 2,

так как k 4+ 6 k ² ≥ 0 и, следовательно, k 4+ 6 k ² + 1 ≥ 1.