Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

9.26.Пусть 7 x − 11 у = u , т. е. 7( x + y ) − 18 у = u , откуда x + y = и + 18 y / 7, а x + 9 у = ( x + y ) + 8 у = и + 74 y / 7.

Приходим к системе

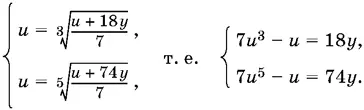
Из последней системы исключим y :

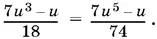
Если u = 0, то, как легко видеть, придем к очевидному решению: x 1= y 1= 0.

Если u ≠ 0, то получаем уравнение

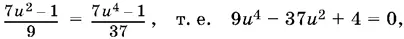
откуда u 1= ⅓, u 2= −⅓, u 3= 2, u 4= −2.

Для каждого значения u составляем систему

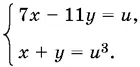
Делаем проверку.

Ответ.(0, 0); ( 10/ 243, − 1/ 243); (− 10/ 243, 1/ 243); (5, 3); (−5, −3).

9.27.Если сложить уравнения системы и вычесть из первого второе, получим систему:

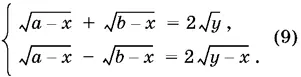
Возведем каждое из уравнений системы (9) в квадрат и вычтем из первого полученного уравнения второе. Получим

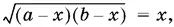
т. е.

( а − x )( b − x ) = x ², или ( а + b ) x = ab .

Если а + b = 0, но ab ≠ 0, то последнее уравнение, а следовательно, и данная система не имеют решений.

Если а + b = 0 и ab = 0, то а = b = 0. Написанная в начале решения система принимает вид

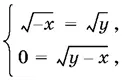
откуда y = − x и y = x одновременно, т. е. при а = b = 0 система имеет единственное решение x = y = 0.

Если а + b ≠ 0, то x = ab / a + b .

Из уравнения 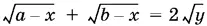находим y :

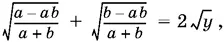
т. е. 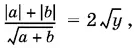откуда y = (| a | + | b |)²/ 4( a + b ).

Так как а + b стоит в предпоследнем уравнении под радикалом и а + b ≠ 0, то а + b > 0.

Преобразовывая систему, мы получили уравнение 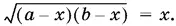Следовательно, x ≥ 0, т. е. ab ≥ 0, а значит, и а ≥ 0, b ≥ 0.

Теперь можно записать, что

y = a + b / 4.

Делаем проверку. Первое уравнение системы после подстановки примет вид

2 а − | а − b | = а + b .

Если а ≥ b , то это уравнение удовлетворяется, а если а < b , то получим а = b , что противоречит предположению а < b .

Второе уравнение системы после подстановки дает равенство 2 b + | а − b | = а + b .

При а ≥ b получаем тождество.

Ответ.Если а ≥ b ≥ 0 и а + b > 0, то x = ab / a + b , y = а + b / 4; если а = b = 0, то x = y = 0.

9.28.Обозначим √ у = z . Тогда система перепишется в виде

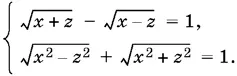
Дважды возведем первое уравнение в квадрат: 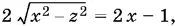отсюда 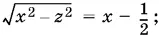далее

4 z ² = 4 х − 1, или z ² = x − ¼.

Заменив 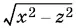выражением x − ½, перепишем второе уравнение системы так:

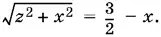
Из последнего уравнения находим z ²:

z ² = 9/ 4− 3 x ,

и сравниваем с выражением для z ², полученным из первого уравнения:

x − ¼ = 9/ 4− 3 x .

Отсюда x = 5/ 8, а y = z ² = 3/ 8.

Проверяем найденные значения x и y . Левая часть первого уравнения системы примет вид

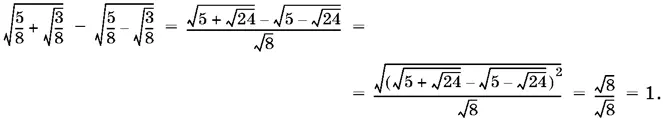
Левая часть второго уравнения вычисляется проще:

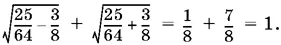
Ответ.( 5/ 8, 3/ 8).

9.29. Способ 1.Так как а и b положительны, то из данных уравнений следует, что x > 0 и y > 0.

Возведем каждое из уравнений в квадрат:

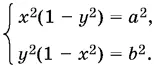
B результате могут быть приобретены только такие посторонние решения, при которых либо x < 0, либо y < 0.

Выражения 1 − y ² и 1 − x ², как это видно из последней системы, останутся положительными.

Мы получили систему относительно x ² = u и y ² = v :

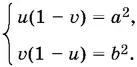
Чтобы эта система была равносильна предыдущей (при замене неизвестных равносильность может быть нарушена!), достаточно потребовать выполнения неравенств

u > 0, v > 0.

Раскрыв в последней системе уравнений скобки, получим

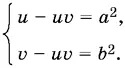
Вычитая из первого уравнения второе, найдем

u − v = а ² − b ²,

т. е. u = v + а ² − b ². Подставим в первое уравнение последней системы, получим квадратное уравнение относительно v :

v ² + ( а ² − b ² − 1) v + b ² = 0,

откуда

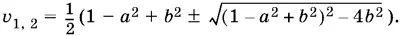
Вычисляем u :

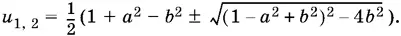
(У u и v , входящих в одно решение, берутся одноименные знаки.)