Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

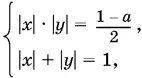
которая при положительных x и y имеет два решения:

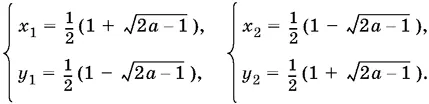
К этим решениям нужно добавить шесть симметричных.

Если а = 1, то y системы четыре решения: x 1= 1, y 1= 0; x 2= 0, y 2= 1; х 3= −1, у 3= 0; х 4= 0, у 4= −1. При а > 1 решений нет.

9.15.Если либо x = 0, либо y = 0, то второе неизвестное тоже равно нулю. Получаем очевидное решение

x 1= 0, y 1= 0.

Если ху ≠ 0, то можно первое уравнение разделить на ху , а второе — на x ² y ². Получим систему

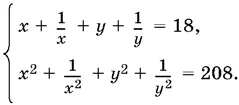
Введем обозначения:

x + 1/ x = u , y + 1/ y= v .

Возводя каждое из этих равенств в квадрат, получим x ² + 1/ x ²= u ² − 2, y ² + 1/ y ²= v ² − 2.

Система примет вид

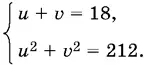
Решая ее, найдем: u 1= 4, v 1= 14; u 2= 14, v 2= 4. (Если первое уравнение возвести в квадрат и сравнить со вторым, то получим uv = 56.) Остается решить две системы:

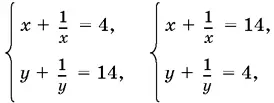
в результате чего получим восемь решений.

Ответ.(0, 0); (2 + √3, 7 + 4√3); (2 + √3, 7 − 4√3); (2 − √3 , 7 + 4√3 ); (2 − √3, 7 − 4√3 ); (7 + 4√3 , 2 + √3); (7 + 4√3, 2 − √3); (7 − 4√3, 2 + √3); (7 − 4√3, 2 − √3).

9.16. Способ 1.Из первого уравнения находим

y − z = ху − x .

Подставляя во второе, получим

xz = 2( x − ху + x ), т. е. xz = 2 x (2 − y ).

Если x = 0, то система принимает вид

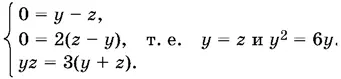
Получаем два решения системы:

x 1= 0, y 1= 0, z 1= 0;

x 2= 0, y 2= 6, z 2= 6.

Если x ≠ 0, то z = 2(2 − y ). Подставляем во второе и третье уравнения

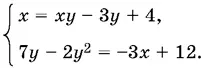
Подставим x из первого уравнения во второе:

7 у − 2 у ² = −3 ху + 9 у .

Если y = 0, то получаем еще одно решение:

x 3= 4, y 3= 0, z 3= 4.

Если y ≠ 0, то 3 x − 2 y = 2, откуда x = 2( y + 1)/ 3. Подставляем в первое уравнение последней системы уравнение, которое превращается в квадратное относительно y :

2 у ² − 9 у + 10 = 0,

откуда y 4= 2, y 5= 3 . Делаем проверку.

Способ 2.Запишем систему в виде

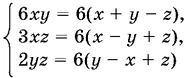
и сделаем три парных сложения

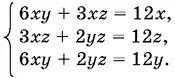
Отсюда находим решения:

а) x = y = z = 0;

б)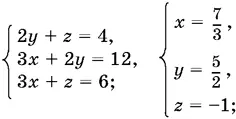

в) если x = 0, то 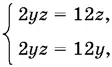y = z = 6;

г) если y = 0, то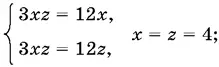

д) если z = 0, то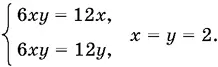

Ответ.(0, 0, 0); (0, 6, 6); (4, 0, 4); (2, 2, 0); ( 7/ 3, 5/ 2, −1).

9.17. Возведем уравнение x + y = − z в квадрат:

x ² + y ² + 2 ху = z ²,

и сравним со вторым уравнением системы; найдем ху = −10.

Преобразуем сумму x 4+ y 4из третьего уравнения следующим образом:

x 4+ y 4= ( x ² + y ²)² − 2 x ² y ² = (20 + z ²)² − 200,

где на последнем шаге были использованы второе уравнение системы и найденное значение для ху . Подставив это выражение в третье уравнение системы, получим

z ² = 9, т. е. z = ±3.

Остается решить каждую из систем:

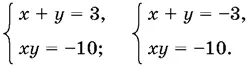
Производим проверку.

Ответ.(−2, 5, −3); (5, −2, −3); (2, −5, 3); (−5, 2, 3).

9.18.Третье уравнение можно записать так:

( x + y )( x ² − ху + y ²) + ( z − 1)( z ² + z + 1) = 0.

Из первого уравнения мы знаем, что x + y = 1 − z . Поэтому

(1 − z )( x ² − ху + y ² − z ² − z − 1) = 0.

Если z = 1, то x + y = 0. Тогда из второго уравнения получим ху = −4. B итоге — два решения:

x 1= 2, y 1= −2, z 1= 1;

x 2= −2, y 2= 2, z 2= 1.

Если же 1 − z ≠ 0, то

x ² − ху + y ² − z ² − z − 1 = 0. (3)

Чтобы упростить уравнение (3), снова воспользуемся тем, что x + y = 1 − z , а потому

x ² + 2 ху + y ² = 1 − 2 z + z ². (4)

Вычитая уравнение (4) из уравнения (3), получим

ху = − z .

Теперь второе уравнение исходной системы

ху + z ( x + y ) = −4

можно переписать как уравнение относительно z

− z + z (1 − z ) = −4.

Решая его, найдем, что либо z = −2, либо z = 2. B первом случае мы приходим к системе

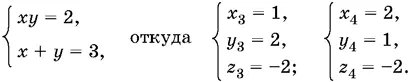
Во втором случае получаем

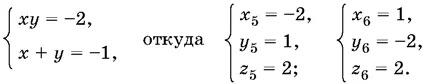
После того как были найдены первые два решения, решение системы можно было закончить следующим рассуждением.

Данная система симметрична относительно x , y и z . Поэтому одно ее решение (2, −2, 1) порождает 3! = 6 решений, получающихся в результате всевозможных перестановок. Таким образом, мы получим шесть различных решений системы.

С другой стороны, можно доказать, что система может иметь не больше решений, чем произведение степеней ее уравнений: 1 · 2 · 3 = 6. Поскольку все шесть решений найдены, решение системы можно считать законченным, если проверить одно из найденных решений.

Ответ.(2, −2, 1); (−2, 2, 1); (1, 2, −2); (2, 1, −2), (−2, 1, 2); (1, −2, 2).

9.19.Рассмотрим многочлен M ( t ) = ( t − x )( t − y )( t − z ) + d . Его корнями по условию являются не совпадающие друг с другом числа а , b и с , следовательно,