Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Возведем последнее иррациональное уравнение в куб. После сокращения получим

4 х (2 x − 3)( x − 1) = 9( x − 1)³.

Один корень этого уравнения x 1= 1; остается квадратное уравнение

x ² − 6 х + 9 = 0, x 2,3= 3.

Сделав проверку, убеждаемся, что найденные корни подходят.

Ответ. x 1= 1; x 2,3= 3.

9.5.Пусть 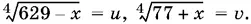Придем к системе

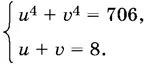
Это — симметрическая система, ее обычно решают подстановкой: и + V = в, ии = _. Поэтому преобразуем левую часть первого уравнения:

u 4+ v 4= ( u ² + v ²)² − 2 u ² v ² = [( u + v )² − 2 uv ]² − 2 u ² v ² = (64 − 2 t )² − 2 t ² = 64² − 256 t + 2 t ².

Поскольку все это равно 706, получаем квадратное уравнение

t ² − 128 t + 1695 = 0,

откуда

t 1= 15, t 2= 113.

Остается решить совокупность двух систем:

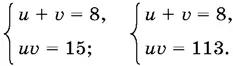
Решая первую, найдем v 1= 3, v 2= 5, откуда x 1= 4, x 2= 548. Вторая не имеет действительных решений.

Проверкой убеждаемся, что найденные корни удовлетворяют исходному уравнению.

Ответ. x 1= 4; x 2= 548.

9.6.Введем новые неизвестные:

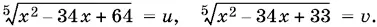
Получим систему

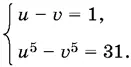
Обозначим u + v = p . Так как в силу первого уравнения системы u − v = 1, то u = p + 1/ 2, v = p − 1/ 2. Второе уравнение системы примет вид

( p + 1/ 2) 5 − ( p − 1/ 2) 5= 31,

или после очевидных упрощений

р 4+ 2 р ² − 99 = 0.

Это биквадратное уравнение имеет два действительных корня р 1= −3, р 2= 3. Зная р 1и р 2, найдем u 1= −1, u 2= 2, откуда получим два уравнения для определения значений x :

x ² − 34 x + 32 = 0, x ² − 34 x + 65 = 0.

Решив эти уравнения, найдем четыре корня.

Ответ.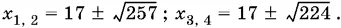

9.7.Введем новые неизвестные:

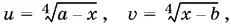
т. е. u 4+ v 4= а − b .

Получаем систему

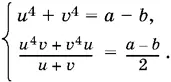
Заменяя во втором уравнении а − b на u 4+ v 4, получим

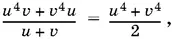
откуда

u 5+ v 5− uv 4− и 4 v = 0, где u + v ≠ 0,

т. е.

u 4( u − v ) − v 4( u − v ) = 0,

а потому

( u − v )²( u ² + v ²)( u + v ) = 0.

Так как последние два множителя в нуль обратиться не могут, то остается и = v , т. е. а − x = x − b , и, следовательно,

x = а + b / 2.

Проверкой убеждаемся, что это — корень исходного уравнения, если а > b .

Ответ.При а > b имеем x = а + b / 2.

9.8.Обозначив 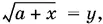получим систему уравнений

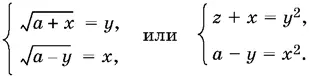
Вычитаем из первого уравнения второе:

x + y = ( y − x )( x + y ).

Если x + y = 0, то x = y = 0, поскольку и x , и y неотрицательны. Так как 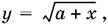то из x = y = 0 следует, что а = 0. Проверкой убеждаемся, что найден корень данного уравнения.

Если x + y ≠ 0, то y − x − 1 = 0, откуда 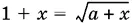и x ² + x + 1 − а = 0. Решая квадратное уравнение, найдем 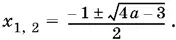Остается исследовать, при каких значениях а эти корни вещественны и удовлетворяют исходному уравнению.

Во-первых, необходимо, чтобы дискриминант был неотрицательным, т. е. а ≥ ¾ .

Во-вторых, корень данного уравнения не должен быть отрицательным. Один из корней 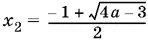при всех а ≥ ¾ отрицателен, а потому не подходит. Другой корень 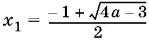больше или равен нулю, если 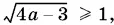т. е. а ≥ 1.

Проверкой убеждаемся, что 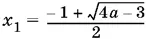удовлетворяет первоначальному уравнению. B самом деле, подставляя x 1в это уравнение, получим 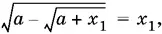что выполняется одновременно с равенством 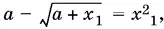так как x ≥ 0. Значение х 1было найдено из уравнения 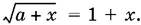Поэтому можно осуществить в полученном нами равенстве соответствующую замену:

a − 1 − x 1= x 1².

Так как в результате мы пришли к уравнению, из которого определили х 1, то проверку можно считать законченной.

Ответ. x = 0, если а = 0, и 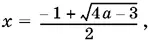если а ≥ 1.

9.9.Перенесем 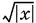в правую часть уравнения:

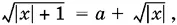
и возведем обе части в квадрат. Получим