Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
что приводит к той же системе уравнений (1) и имеет место при а = −4, b = 1. Следовательно, x = 1 − √3 — второй корень данного в условии уравнения.
Разделив многочлен x 4− 4 x ³ + x ² + 6 x + 2 на
( x − √3 − 1)( x + √3 − 1) = x ² − 2 x − 2,
получим квадратный трехчлен x ² − 2 x − 1, корнями которого являются числа 1 + √2.
Ответ. x 1,2= 1 ± √3; x 3, 4= 1 ± √2.
8.8.Из теоремы Виета получаем неравенства:
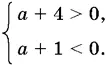
Добавляем к ним условие неотрицательности дискриминанта:
( а + 1)² − 4( а + 4) ≥ 0.
Приходим к системе неравенств
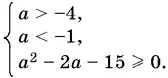
Последнему неравенству удовлетворяют числа а , лежащие вне промежутка между корнями: а ≤ −3, а ≥ 5.
Ответ.−4 < а ≤ −3.
8.9.Пусть х 1, х 1 q и х 1 q ² — корни данного уравнения. По теореме Виета имеем систему
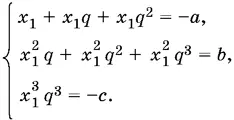
Из этих уравнений нужно исключить x 1и q . Поскольку из первого уравнения следует х 1(1 + q + q ³) = − а , то второе примет вид
b = х 1² q (1 + q + q ²) = x 1 q (−а),
т. е. x 1 q = − b / a , откуда
− b ³/ a ³= − c .
Ответ. са ³= b ³.
8.10.По теореме Виета
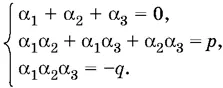
Возведем первое уравнение в квадрат:
α 1² + α 2² + α 3² + 2(α 1α 2+ α 1α 3+ α 2α 3) = 0,
откуда найдем α 1² + α 2² + α 3² . Как видим, последнее уравнение не понадобилось.
Ответ.α 1² + α 2² + α 3² = −2 p .
8.11.Разделив x ³ + ax + 1 на x − α, получим в частном x ² + α x + а + α², а в остатке α³ + a α + 1. Условия задачи будут выполняться тогда и только тогда, если
α³ + a α + 1 = 0,
x ² + α x + а + α² > 0 при всех x .
Чтобы выполнялось второе условие, дискриминант −3α² − 4 а должен быть отрицательным, т. е. 3α² + 4 а > 0.
Число а не может быть равно нулю, так как уравнение а ³ + а α + 1 = 0 не удовлетворяется при а = 0. Из первого уравнения a = − 1 + α³/ α. Поэтому должно быть
3α² − 4 1 + α³/ α> 0.
Если α > 0, то последнее неравенство эквивалентно такому:
3α³ − 4(α³ + 1) > 0,
или −α³ > 4, y которого нет решений.
Если α < 0, то получим
3α³ − 4(α³ + 1) < 0,
или 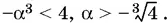
Ответ. 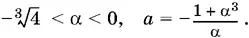
8.12.Пусть
P ( x ) = ( x − 2)( x − 3) Q ( x ) + ax + b ,
где ax + b — остаток, который надо найти.
По теореме Безу P (2) = 5, а P (3) = 7. Подставим x = 2 и x = 3 в правую часть написанного выше тождества. Получим систему относительно а и b
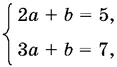
откуда а = 2, b = 1.
Ответ.2 x + 1.
8.13.Многочлен x 4+ 1 делится на x ² + рх + q тогда и только тогда, когда
x 4+ 1 = ( x ² + ax + b )( x ² + рх + q ).
Раскрывая в правой части скобки и приравнивая коэффициенты при одинаковых степенях x , получим систему уравнений
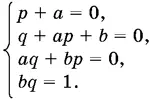
Из первого и последнего уравнений находим а = − p , b = 1/ q . Подставляя в оставшиеся два уравнения, получим
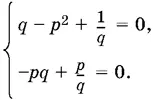
Второе уравнение можно переписать так: p ( q − 1/ q ) = 0.
Если p = 0, то первое уравнение не имеет действительных решений. Остается q = 1/ q , т. е. q = ±1. Подставляя найденные значения q в первое уравнение, увидим, что, когда q = 1, р ² = 2 и p = ±√2, а когда q = −1, р ² = −2 и действительных решений нет. Итак, получаем две возможности: либо p = √2 и q = 1, либо p = −√2 и q = 1.
Чтобы закончить решение, нужно сделать проверку. Можно было бы разделить x 4+ 1 поочередно на каждый из двух трехчленов: x ² + √2 x + 1 и x ² − √2 x + 1. Однако проще убедиться, что
x 4+ 1 = ( x ² + √2 x + 1)( x ² − √2 x + 1).
Ответ. р 1= − √2, q 1= 1; р 2= √2, q 2= 1.
8.14.После замены x − 1 = y получим многочлен
( y + 1) 2 n + 1− (2 п + 1)( y + 1) n + 1+ (2 п + 1)( y + 1) n − 1,
который должен делиться на y ³. Вычислим его коэффициенты при y 0, y 1и y 2.
Свободный член этого многочлена равен
1 − (2 n + 1) + (2 n + 1) − 1 = 0;
коэффициент при y
2 n + 1 − (2 n + 1)( n + 1) + (2 n + 1) n = 0;
коэффициент при y ²
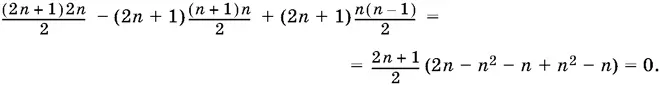
Тем самым утверждение доказано.
8.15.Чтобы данный многочлен делился на x ² − x + q без остатка, должно выполняться тождество
6 х 4− 7 x ³ + рх ² + 3 x + 2 = ( x ² − x + q )(6 х ² + ax + b ).
B правой части стоит многочлен
6 x 4+ ( а − 6) x ³ + ( b − а + 6 q ) x ² + (− b + qа ) x + qb .
Так как многочлены равны тождественно, получаем систему
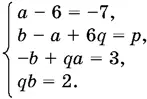
Из первого уравнения а = −1. Из третьего и четвертого уравнений исключаем b . Приходим к уравнению
q ² + 3 q + 2 = 0,
откуда
q 1= −1, q 2= −2.
Сложив второе и третье уравнения, также исключим b :
5 q − 2 = p .
Следовательно,
р 1= −7, p 2= −12.
Итак, возможны два решения.
Ответ. 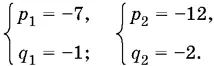
Глава 9
Алгебраические уравнения и системы
Ответык упражнениям на с. 42, 43 и 52.
1.Абсолютное тождество, так как верно при всех без исключения значениях x .
2.Абсолютное тождество. Верно при x ≠ π/ 2+ k π. Если же x = π/ 2+ k π, то обе части теряют смысл.
Читать дальшеИнтервал:
Закладка:










