Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

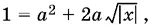
откуда при а ≠ 0

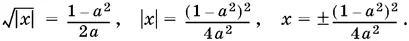
Делаем проверку, подставляя найденное значение x в данное уравнение. B левой части получим

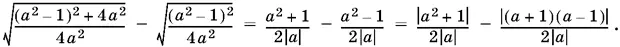
Чтобы вычислить это выражение, нужно рассмотреть четыре различных случая, так как значения −1, 0, +1 параметра а разбивают числовую ось на четыре интервала. Однако легко заметить, что а > 0, так как разность, стоящая в левой части исходного уравнения, всегда положительна. Следовательно, остается рассмотреть только два случая.

Если 0 < а ≤ 1, то

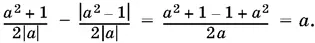
Если же а > 1, то

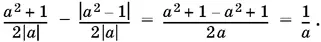
Число 1/ а равно числу а только при а = ±1, а по предположению а > 1.

Ответ. 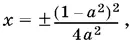если 0 < а ≤ 1.

9.10.Рассмотрим два случая.

Если 2 x ² − 3 x − 2 ≥ 0, т. е. x ≤ −½, x ≥ 2, получим уравнение

4 х ² + 5 х − 2(1 + β) = 0.

Корни этого уравнения 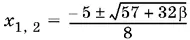должны лежать вне интервала (−½, 2).

Неравенство

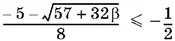
удовлетворяется при β ≥ − 57/ 32. Больше двух этот корень быть не может.

Для x 2нужно решить два неравенства:

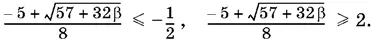
Первое выполняется при − 57/ 32 ≤ β ≤ − 7/ 4, а второе — при β ≥ 12.

Пусть теперь 2 x ² − 3 x − 2 < 0, т. е. −½ < x < 2. Данное уравнение станет линейным и мы найдем

x 3= 2(β − 1)/ 11.

Решим неравенство

−½ < 2(β − 1)/ 11 < 2

и получим

− 7/ 4< β < 12.

Итак, при β = − 57/ 32корни х 1и х 2совпадают, а корень х 3не существует, т. е. уравнение имеет единственное решение x = − 5/ 8. Если − 57/ 32 < β ≤ − 7/ 4, то уравнение имеет два решения: х 1и х 2(которые, очевидно, различны); если − 7/ 4< β ≤ 12, то х 1и х 3; а если β ≥ 12, то два решения: х 1и х 2.

Корни х 1и х 3различны, так как −½ < х 3< 2, а х 1лежит вне этого интервала.

Ответ. β = − 57/ 32.

9.11.Если x ≥ 0, y ≥ 0, то получим систему

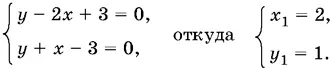
Если x ≥ 0, y ≤ 0, то

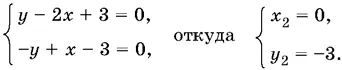
Если x ≤ 0, y ≥ 0, то

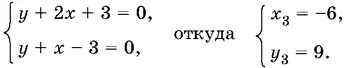
Если x ≤ 0, y ≤ 0, то

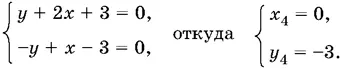
Каждое из четырех решений удовлетворяет записанным ограничениям.

Ответ.(2, 1); (0, −3); (−6, 9); (0, −3).

9.12.Исключая последовательно y и x , найдем

x = k + 16/ 7, y = 8 − 3 k / 7.

Остается решить систему неравенств

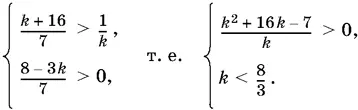
Первое неравенство равносильно такому:

( k + 8 + √71 )( k + 8 − √71 ) k > 0.

Приходим к системе

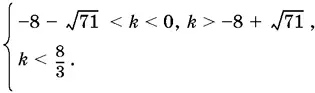
Так как −8 + √71 < 8/ 3, то условию задачи удовлетворяют два интервала.

Ответ.−8 − √71 < k < 0; −8 + √71 < k < 8/ 3.

9.13.Если x ≥ − у и x ≥ y , то получим системы

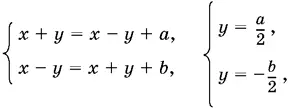
которая при x ≥ − у и x ≥ y имеет решение

x ≥ | a |/ 2, y = а / 2

при условии а = − b .

Если x ≥ − у , но x ≤ y , то

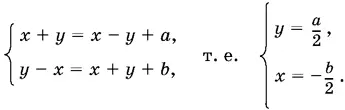
Из условия x ≥ − у находим − b / 2 ≥ − а / 2, а из второго условия: − b / 2≤ а / 2. Оба этих неравенства соответствуют условию а ≥ | b |.

Если x ≤ − у , а x ≥ y , то

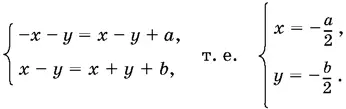
Подставляя найденные значения x и y в ограничения, получим b ≥ | а |.

Наконец, если x ≤ − у , x ≤ y , получим

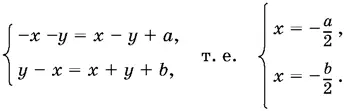
Это значит, что а = b. Так как y ≥ x , но y ≤ − х , то − x ≥ 0. Окончательно получим при а = b ≥ 0

x = − а / 2, − а / 2 ≤ y ≤ а / 2.

Ответ.При а = − b , x ≥ | а |/ 2, y = а / 2; при а ≥ | b |, x = − b / 2, y = а / 2; при b ≥ | a |, x = − а / 2, y = − b / 2; при а = b ≥ 0, x = − а / 2, − а / 2 ≤ y ≤ а / 2.

9.14. Уравнение x ² + y ² = а при а < 0 не имеет решений. Если а ≥ 0, то это — уравнение окружности радиуса √ a с центром в начале координат. Второе уравнение определяет стороны квадрата, диагонали которого равны 2 и расположены на осях координат (рис. P.9.14).

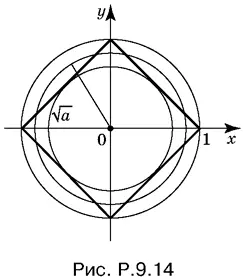
При увеличении а окружность будет увеличиваться и сначала окажется вписанной в квадрат, затем пересечет его в восьми точках и, наконец, будет описана около квадрата.

Итак, если √ а < √2/ 2, то система не имеет решений.

Если √ а = √2/ 2, т. е. а = ½, получим четыре решения: x = ½, y = ½ и три симметричных: (−½, ½), (−½, −½), (½, ½).

Если ½ < а < 1, то восемь решений. Мы найдем их, возведя первое уравнение в квадрат и получив с помощью второго уравнения, что | x | · | y | = 1 − a / 2. B результате придем к системе