Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
M ( t ) = ( t − а )( t − b )( t − с ), или ( t − а )( t − b )( t − с ) ≡ ( t − x )( t − y )( t − z ) + d .
Приравнивая коэффициенты при одинаковых степенях t , найдем
x + y + z = а + b + с = u ,
ху + хz + уz = ab + ас + bc = v ,
xyz = аbс + d = w
(справа указаны вводимые нами обозначения).
Поскольку нужно найти сумму x ³ + y ³ + z ³, выразим ее через u , v и w , осуществив непосредственное возведение в куб суммы x + y + z = u :
u ³ = x ³ + y ³ + z ³ + 3 uv − 3 w (5)
(необходимые выкладки проведите самостоятельно). Запишем теперь то же соотношение для а + b + с = u и тем самым выразим а ³ + b ³ + с ³ через u , v и w :
u ³ = а ³ + b ³ + с ³ + 3 uv − 3( w − d ). (6)
Вычитая из (6) соотношение (5), получим
x ³ + y ³ + z ³ = а ³ + b ³ + с ³ + 3 d .
Ответ. а ³ + b ³ + с ³ + 3 d .
9.20.Умножив первое уравнение на ху ² z ², а второе — на x ² уz ², получим y первых двух уравнений равные правые части:
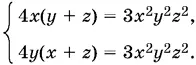
При этом могут быть получены посторонние решения, y которых одно из неизвестных обращается в нуль. Эти решения можно сразу отбросить, так как система в этом случае не удовлетворяется.
Сравним левые части полученных уравнений:
4 z ( x − y ) = 0.
Так как z ≠ 0, то x = y . Из третьего уравнения системы получаем тогда z = 1/ x ³. Подставим эти значения y и x в первое уравнение:
4 х 4+ 1 = 0. (7)
Уравнение (7) не имеет действительных решений.
Ответ.Действительных решений нет.
9.21.Возведя второе уравнение в квадрат, найдем
( x + y )² = x ² y ²/ 4.
Подставим в первое уравнение
x 4+ y 4= 17/ 4 x ² y ², т. е. ( x ² − y ²)² = 9/ 4 x ² y ²,
откуда
x ² − y ² = ± 3/ 2 ху ,
или, воспользовавшись вторым уравнением исходной системы, получим
x ² − y ² = ±3( x + y ),
откуда
( x + y )( x − y ± 3) = 0.
Если x + y = 0, то и ху = 0, следовательно,
x 1= 0, y 1= 0.
Если x − y = 3, то, подставляя во второе уравнение данной системы y = x − 3, придем к уравнению x ² − 7 x + 6 = 0, с помощью которого найдем два решения системы:
x 2= 1, y 2= −2;
x 3= 6, y 3= 3.
Если же x − y = −3, то аналогично получим
x 4= −2, y 4= 1;
x 5= 3, y 5= 6.
Производим проверку.
Ответ.(0, 0); (1, −2); (6, 3); (−2, 1); (3, 6).
9.22.Умножим первое уравнение на t :
хt + уt = t
и вычтем из второго. Аналогично поступим со вторым и третьим уравнениями. Придем к системе, не содержащей y :
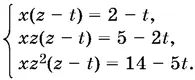
B результате могут быть получены посторонние решения, в которых t = 0. Однако решение нашей системы мы закончим проверкой, благодаря которой все посторонние решения будут отсеяны.
Если x = 0, то одновременно 2 − t = 0 и 5 − 2 t = 0, что невозможно. По аналогичной причине z − t ≠ 0, z ≠ 0.
Поделим теперь второе уравнение последней системы на первое, а третье на второе. Получим
z = 5 − 2 t / 2 − t , z = 14 − 5 t / 5 − 2 t .
Приравнивая эти выражения для z , придем к квадратному уравнению относительно t :
t ² − 4 t + 3 = 0, т. е. t 1= 1, t 2 = 3.
Итак, z 1= 3, z 2= 1.
Остается определить x и y и сделать проверку.
Система имеет два решения.
Ответ.(½, ½, 3, 1) (½, ½, 1, 3).
9.23.Возведем первое уравнение в квадрат и вычтем из второго уравнения. После упрощения получим
2 ху − 3 хz + 6 уz = 54.
Третье уравнение позволяет заменить 3 xz на 4 у ²:
2 ху − 4 у ² + 6 уz = 54, или ху − 2 у ² + 3 уz = 27. (8)
Вычтем из уравнения (8) первое уравнение системы, умноженное на y [17] Такое преобразование системы, вообще говоря, может привести к приобретению постороннего решения, в котором y = 0.
, получим
y = 3.
Подставим в первое и третье уравнения системы
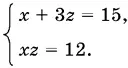
Решая эту систему, найдем два решения:
x 1= 3, z 1= 4; x 2= 12, z 2= 1.
Производим проверку.
Ответ.(3, 3, 4); (12, 3, 1).
9.24.Сложив первое уравнение со вторым, первое с третьим и, наконец, второе с третьим, получим систему
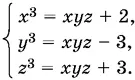
Перемножим эти уравнения и обозначим xyz = u :
u ³ = ( u + 2)( u ² − 9),
а после упрощения
2 u ² − 9 u − 18 = 0,
откуда u 1= 6, u 2= − 3/ 2.
Для первого значения u находим x ³ = 8, y ³ = 3, z ³ = 9, аналогично поступаем с u 2. Производим проверку.
Ответ. 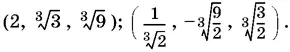
9.25.Обозначим x 1+ x 2+ ... + x n = s . Тогда уравнение, стоящее на месте с номером k , примет вид
x k ( s − x k ) + k ( k + 1) s ² = (2 k + 1)² а ²,
или
x k ² − sx k − k ( k + 1) s ² + (2 k + 1)² a ² = 0,
откуда
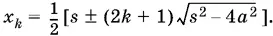
Возьмем для всех x k знак минус и составим сумму х 1+ ... + x n . Получим уравнение относительно в
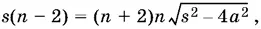
откуда
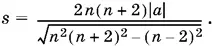
Мы взяли перед корнем знак плюс, так как из уравнения для в видно, что s > 0; знаменатель не обращается в нуль ни при каких натуральных h .
Остается подставить найденное значение в в выражение для x k и сделать проверку.
Ответ. 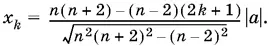
Интервал:
Закладка:










