Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.±1.

9.32.Так как система должна иметь хотя бы одно решение при любом b , то она должна иметь решение и при b = 0. Положив b = 0, получим систему

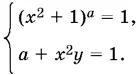
Первое уравнение удовлетворяется либо при а = 0 и любом x , либо при x = 0. Если x = 0, то из второго уравнения получаем а = 1. Итак, возможны только два значения: а = 0 и а = 1.

При а = 0 получаем систему

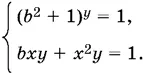
Первое уравнение имеет решение при любом b , только если y = 0. Однако это значение y не удовлетворяет второму уравнению.

Остается рассмотреть случай а = 1. Система примет вид

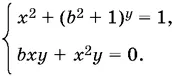
При любом b эта система имеет решение x = y = 0.

Ответ.1.

9.33.Пусть ( х 1, у 1) — решение системы. Тогда второе уравнение удовлетворяется еще тремя парами значений неизвестных (− x 1, y 1), ( x 1, − y 1), (− x 1, − y 1). Легко убедиться, что первое уравнение наряду с ( x 1, y 1) имеет также решение ( x 1, − y 1):

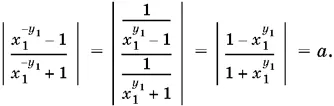
Таким образом, система может иметь единственное решение лишь при условии, что y 1= − y 1, т. е. y = 0. Подставим это значение y в систему. Из первого уравнения получим а = 0.

Выясним, достаточно ли условия а = 0 для единственности решения исходной системы. Если а = 0, то x y = 1, а это означает, что либо x = 1, y — любое число, либо x ≠ 0 — любое, y = 0. Значения параметра b должны быть такими, чтобы второму уравнению системы удовлетворяло только одно из решений первого. Если y = 0, то второе уравнение имеет единственное решение x = √ b (по условию x > 0) при любом b > 0. Поэтому b нужно выбрать таким, чтобы исключить случай x = 1, т. е. таким, чтобы уравнение 1 + y ² = b не имело действительных решений. Для этого необходимо и достаточно выполнение ограничения b < 1.

Если x = 1, то второе уравнение имеет единственное решение в том и только в том случае, если b = 1. При этом ему удовлетворяет единственное из решений первого уравнения: x = 1, y = 0.

Ответ. а = 0, 0 < b ≤ 1.

9.34.Умножим числитель и знаменатель дроби из второго уравнения на 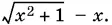Полученное уравнение разделим на y , который тоже отличен от нуля, если входит в решение системы. Получим 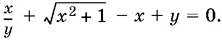Исключим 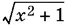с помощью первого уравнения системы:

x ²/ y ²− 2 x / y + y ² + 2 x − 2 y = 3.

Последнее уравнение перепишем в виде

x ²/ y ²+ 2 x + y ² − 2( x / y + y ) = 3

Если x + y = z , то z ² − 2 z − 3 = 0, z 1= −1, z 2= 3. Первое уравнение данной системы можно записать в виде

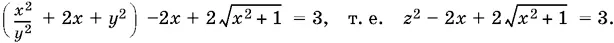
Если 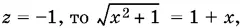откуда x = 0. Второе уравнение системы дает тогда два значения: y 1= 0, y 2= −1, где y = 0 не удовлетворяет первому уравнению. Если z = 3, то x = 4/ 3; второе уравнение системы после несложных преобразований принимает вид 3 y ²+ y + 4 = 0, т. е. не имеет действительных решений.

Проверка убеждает нас в том, что x = 0, y = −1 — единственное решение системы.

Ответ.(0, −1).

9.35.Запишем данное уравнение в виде

|6 − | x − 3| − | x + 1|| = а ( x + 5) + 4. (10)

Построим график функции

y = |6 − | x − 3| − | x + 1||. (11)

Начнем с графика функции

y = 6 − | x − 3| − | x + 1|, (12)

который легко построить, разбив числовую ось на три интервала точками x = −1, x = 3 (рис. P.9.35).

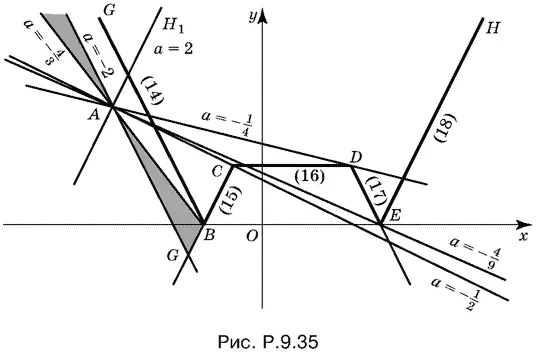
Получим

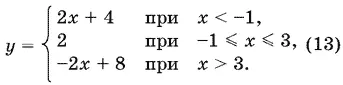
Этот график совпадает с графиком функции (11) там, где значения y , полученные из (13), неотрицательны. Если же значения y , полученные из (13), отрицательны, то им соответствуют симметричные относительно оси Ox точки графика. Таким образом, для интервала −2 ≤ x ≤ 4 графики функций (11) и (12) совпадают, а при x < −2 и при x > 4 мы получаем симметричные относительно оси Ox лучи. В итоге для функции (11) имеем:

График этой функции изображен на рис. P.9.35 жирной линией (около каждого отрезка указан номер соответствующего ему уравнения).

Если подойти к задаче формально, то мы можем рассчитать точки пересечения прямой (19) — см. ниже — с каждой из прямых (14), (15), (16), (17), (18). Получим соответственно:

x 1= − 5 a + 8/ a + 2, x 2= 5 a / 2 − a , x 3= − 5 a + 2/ a , x 4 = 4 − 5 a / a + 2, x 5= 5 a + 12/ 2 − a .

Рассмотрим теперь при разных значениях параметра а семейство прямых

y = а ( x + 5) + 4 (19)

и определим, сколько точек пересечения y каждой из прямых (19) с графиком функции (13).

Тангенс угла наклона прямых (19) равен а и все эти прямые проходят через точку А (−5; 4). Обозначим на графике точки В (−2; 0), С (−1; 2), D (3; 2), E (4; 0), а также точки G и H , расположенные на левом и правом лучах графика (11) соответственно. Соединим точку А(−5; 4) с точками /(−2; 0), С(−1; 2), 1(3; 2) и E(4; 0). Проведем через точку А прямые AG 1 || EH . Обозначим на каждой из проведенных нами через точку А прямых ее угловой коэффициент а : для AC имеем а = −2, для AB , AC , AE , AD и AH 1соответственно а принимает значения: − 4/ 3, −½, − 4/ 9, ¼, 2.

Теперь нетрудно подсчитать, при каких а какие решения имеет данное в условии уравнение. Получим