Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

10.2.Обозначим произведение, стоящее в левой части неравенства, через P . Так как а 1 а 2... а n = 1, то

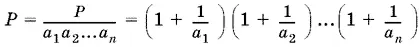
(осуществлено почленное деление суммы 1 + а i на а i ). Поскольку

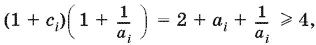
то P ² ≥ 4 n и, следовательно, P ≥ 2 n , что и требовалось доказать.

10.3. Способ 1.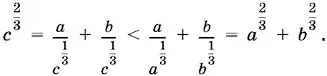

Способ 2.Неравенству a ⅔ + b ⅔> c ⅔ эквивалентно неравенство

( a / c ) ⅔+ ( b / c ) ⅔> 1.

Так как b < с и а < с , то основания показательных функций ( a / c ) x и ( b / c ) x меньше единицы и эти функции убывают. Следовательно,

( a / c ) ⅔+ ( b / c ) ⅔> a / c + b / c = 1.

10.4.Данное неравенство можно переписать так:

4 x ³ − 4 x ² + 1 ≥ 0.

Оценим левую часть:

4x²( x − 1) + 1 = −4x²(1 − x ) + 1.

Так как 0 ≤ x ≤ 1, то x ² ≤ x и 1 − x ≥ 0. Следовательно,

−4x²(1 − x ) + 1 ≥ −4x(1 − x ) + 1 = (2 x − 1)² ≥ 0,

что и доказывает наше неравенство.

10.5.Каждый из входящих в неравенство корней оценим следующим образом:

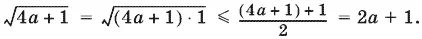
Складывая полученные неравенства, придем к выводу, что

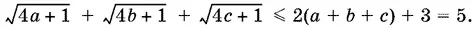
Теперь, чтобы доказать написанное в условии неравенство, остается убедиться, что в последней оценке равенство никогда не достигается. Равенство возможно лишь при одновременном выполнении равенств 4 a + 1 = 1, 4 b + 1 = 1, 4 с + 1 = 1, т. е. при а = b = с = 0, что противоречит условию а + b + с = 1.

Итак,

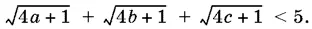
10.6.Пусть b < а . Тогда

( а + b ) n ≤ (2 a ) n = 2 na n < 2 n ( a n + b n ).

10.7.Так как ( а / b ) x − возрастающая показательная функция (по условию а > b ) и p > q , то

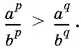
Воспользовавшись формулой производной пропорции, получим

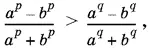
что и требовалось доказать.

10.8.Имеем n очевидных неравенств:

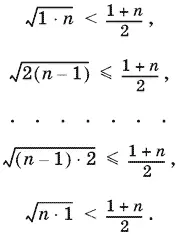
Первое и последнее неравенства обязательно будут строгими, так как по условию n > 1. Перемножая эти неравенства, получим

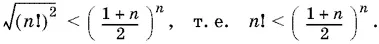
10.9. Способ 1.Обозначим a / b = u , b / c = v , c / a = w . Тогда uvw = 1, т. е. среди чисел u , v и w есть хотя бы одно, большее 1, и одно, меньшее 1 ( u = v = w невозможно, так как а , b и с не равны друг другу). Пусть u > 1, а 0 < v < 1, т. е.

(1 − u )( v − 1) > 0 или − uv + u + v − 1> 0.

С другой стороны, для чисел u , v и e выполняется неравенство

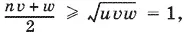
т. е. uv + w ≥ 2. Складывая это неравенство с неравенством − uv + u + v − 1 > 0, получим

u + v + w > 3, или a / b + b / c + c / a > 3.

Способ 2.Пусть u , v и w — положительные числа, причем w — наименьшее из них: u > w , v > w . Так как u и w — положительные числа, то на них можно умножить неравенство v > w :

v ( u − w ) > w ( u − w ), т. е. uv − vw + w ² > uw .

Поделим последнее неравенство на uw :

v / w − v / u + e / u > 1.

С другой стороны,

u / v + v / u ≥ 2.

Складывая с предыдущим неравенством, получим

u / v + v / w + w / u > 3.

Если с — наименьшее из чисел а , b и с , то полагаем w = с , u = а , v = b и получаем неравенство, которое требовалось доказать. Если а или b — наименьшее из чисел а , b и с , то обозначения соответственно изменятся.

Способ 3.Пусть b = с + d 1, а = b + d 2( d 1> 0, d 2> 0, т. е. а > b > с ). Тогда

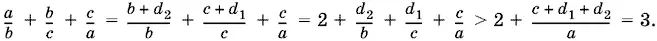
Это решение обобщается на случай n чисел:

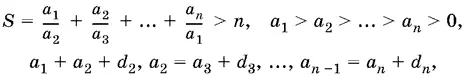
т. е.

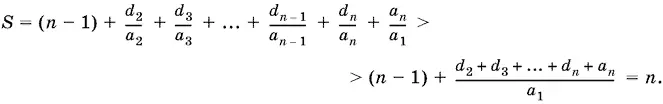
10.10.Воспользуемся формулой Герона и применим к сомножителям p − а , p − b , p − с неравенство между средним геометрическим и средним арифметическим трех чисел ( p − а + p − b + p − с = 3 p − 2 p = p ):

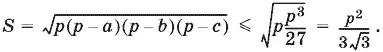
В условие входит величина 4 S , для которой мы и проведем дальнейшие оценки

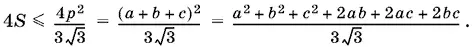
Выделим в числителе слагаемое 3( а ² + b ² + с ²), а излишек в 2( а ² + b ² + с ²) используем для образования полных квадратов, которые поглотили бы все попарные произведения:

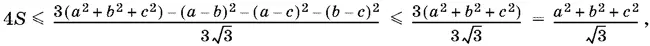
и тем самым неравенство доказано.

10.11.Оценим левую часть неравенства:

( x − 1)( x − 3)( x − 4)( x − 6) + 10 = ( х ² − 7 х + 6)( х ² − 7 х + 12) + 10 = [( х ² − 7 х + 9) − 3][( х ² − 7 х + 9) + 3] + 10 = ( х ² − 7 х + 9)² − 9 + 10 = ( х ² − 7 х + 9)² + 1 ≥ 1.

10.12.Подставляя в первое уравнение x ² вместо yz , преобразуем систему следующим образом:

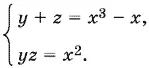
Числа y и z являются корнями квадратного уравнения относительно u :