Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.Неравенство не имеет решений.

10.22.Данное неравенство можно переписать так:

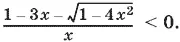
Получаем совокупность двух систем

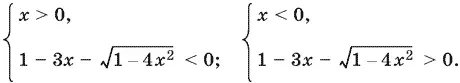
Решаем первую систему

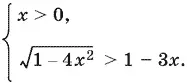
Если правая часть второго неравенства отрицательна ( x > ⅓), то неравенству будут удовлетворять все x , при которых подкоренное выражение неотрицательно ( x ² ≤ ¼, | x | ≤ ½). Получаем интервал решений ⅓ < x ≤ ½.

Если правая часть второго неравенства неотрицательна ( x ≤ ⅓), то второе неравенство можно возвести в квадрат (дополнять систему условием 1 − 4 x ² ≥ 0 или | x | ≤ ⅓ не нужно). После простых преобразований получим

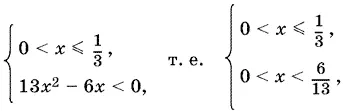
откуда 0 < x ≤ ⅓. Объединяя интервалы 0 < x ≤ ⅓ и ⅓ < x ≤ ½, получим решение первой системы: 0 ≤ x ≤ ½.

Перейдем ко второй системе:

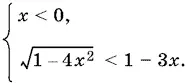
Условие x < 0 обеспечивает положительность правой части второго не равенства. Возведем второе неравенство в квадрат, учитывая, что | x | ≤ ½. Получим

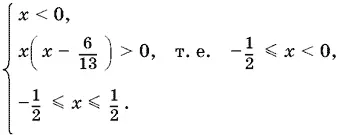
Ответ.−½ ≤ x < 0, 0 < x ≤ ½.

10.23.Перепишем данное неравенство в виде

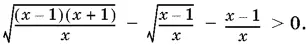
Так как в неравенство входит выражение 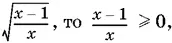а потому 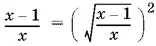. Вынесем множитель 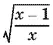за скобки:

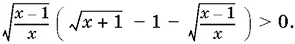
Это неравенство равносильно системе

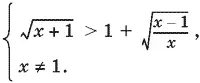
Возведем первое неравенство системы в квадрат. При этом следует добавить условие, в силу которого выражение, «освободившееся» от влияния радикала, должно быть неотрицательным:

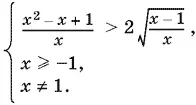
Так как x ² − x + 1 > 0 при всех x , то первому неравенству системы могут удовлетворять только x > 0, ибо выражение справа всегда положительно. Следовательно, систему можно переписать в виде

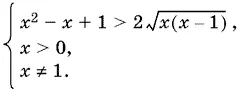
Обозначим 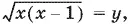тогда первое неравенство примет вид y ² − 2 y + 1 > 0, т. е. ( y − 1)² > 0, откуда y ≠ 1. Итак,

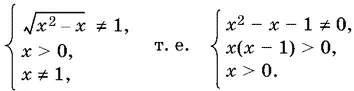
Последняя система равносильна такой:

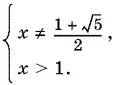
Ответ.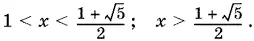

10.24.При x > 0 правая часть неравенства положительна, так как в этом случае 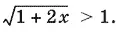Возведем обе части неравенства в квадрат; получим систему

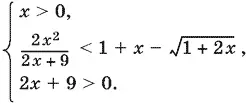
Последнее неравенство системы — следствие того, что x > 0. Перенесем во втором неравенстве 1 + x в левую часть и произведем некоторые упрощения. Получим систему

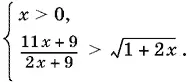
Так как x > 0, то второе неравенство можно возвести в квадрат, не добавляя при этом никаких ограничений (убедитесь в этом самостоятельно):

121 x ² + 198 x + 81/ 4 x ² + 36 x + 81> 1 + 2 x .

Умножим неравенство на знаменатель, который при x > 0 положителен; после приведения подобных получим систему

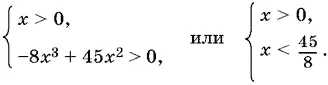
Итак, в первом случае неравенство имеет решения: 0 < x < 45/ 8.

При x = 0 данное неравенство не удовлетворяется.

Если же x < 0, то, умножив обе части на −1, придем к неравенству

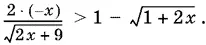
Проделав с этим неравенством преобразования, аналогичные случаю, когда x > 0, придем к выводу, что оно не имеет решений при отрицательных x .

Ответ.0 < x < 45/ 8.

10.25.Перепишем данное неравенство в виде

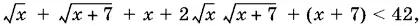
т. е.

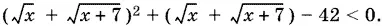
Обозначив выражение, стоящее в скобках, через y , получим квадратное неравенство

y ² + y − 42 < 0,

которое имеет решения: −7 < y < 6. Итак,

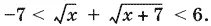
Поскольку сумма 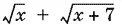всегда положительна, то достаточно решить лишь правое неравенство:

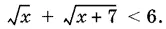
После возведения в квадрат получим неравенство

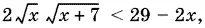
равносильное исходному, так как корни √ x и 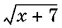здесь не устранены. (Заметьте, что, заменив выражение √ x 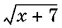на 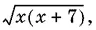мы могли нарушить равносильность.) После второго возведения в квадрат придем к системе