Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

y < −1, y > 0.

Вспоминая, что y = log k x и 0 < k < 1, найдем соответствующие интервалы для x .

Ответ.0 < x < 1, x > 1/ k .

10.40.Поскольку 4 x − 6 должно быть больше нуля, то x > 1. Следовательно, приходим к системе неравенств

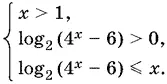
Решая второе неравенство системы, найдем x > log 2√7.

Третье неравенство перепишем в виде системы

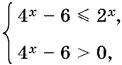
решением которой будет интервал log 2√6 < x ≤ log 23. Так как log 2√7 > log 2√6, то получим решение данного неравенства.

Ответ.log 2√7 < x ≤ log 23.

10.41.Данное неравенство эквивалентно такому:

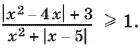
Знаменатель всегда положителен. Поэтому

| х ² − 4 x | + 3 ≥ x ² + | x − 5|,

остается раскрыть знаки абсолютной величины. Нанесем точки 0, 4, 5 на числовую ось и рассмотрим четыре случая.

Если x < 0, то получаем систему

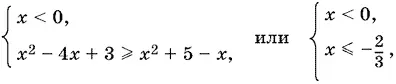
которой удовлетворяет полупрямая x ≤ −⅔.

Если 0 ≤ x ≤ 4, приходим к системе

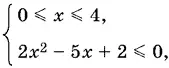
решением которой будет отрезок 1 < x < 2.

Если 4 < x ≤ 5, то наше неравенство примет вид x ² − 4 x + 3 ≥ x ² + 5 − x , откуда x ≤ −⅔. Это не удовлетворяет условию 4 < x ≤ 5, а потому в данном случае решений нет.

Остается случай x > 5. Раскрывая знаки абсолютных величин, получим x ≤ 8/ 5. Здесь снова нет решений.

Ответ. x < −⅔; ½ ≤ x ≤ 2.

10.42.Из условия следует, что x > 2. Поэтому x ³ − 7 > 0, а также x − 1 > 1 и (x − 1)² > 1. Данное неравенство равносильно такому:

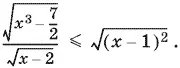
Так как x − 1 > 0, то 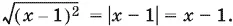Поскольку x ³ − 7/ 2> 0, то ограничение x > 2 достаточно для того, чтобы следующие преобразования приводили к равносильным неравенствам:

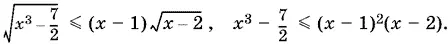
После упрощений последнее неравенство сведется к квадратному: −4 x ² + 5 x + 3/ 2 ≥ 0, имеющему решения −¼ < x < 3/ 2. Так как, кроме того, x > 2, то исходное неравенство не имеет решений.

Ответ. Решений нет.

10.43.Так как первый сомножитель положителен, то, чтобы неравенство удовлетворялось, необходимо

log 2(2 − 2 x ²) > 0, т. е. 2 − 2 x ² > 1, √2| x | < 1,

откуда

0 ≤ √2| x | < 1 и −1 ≤ √2| x | − 1 < 0.

Следовательно, |√2| x | − 1| ≤ 1. Таким образом, первоначальное неравенство может удовлетворяться только, если

log 2(2 − 2 x ²) ≥ 1, или 2 − 2 x ² ≥ 2, − x ² ≥ 0,

т. е. x = 0. Проверкой убеждаемся, что x = 0 является решением неравенства.

Ответ. x = 0.

10.44.Так как , то перепишем неравенство следующим образом:

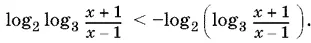
Обозначив log 3 x + 1/ x − 1= y , получим log 2 y < 0, откуда

0 < y < 1, т. е. 0 < log 3 x + 1/ x − 1< 1,

а потому 1 < x + 1/ x − 1< 3.

Последнее неравенство можно записать так:

( x + 1/ x − 1− 1)( x + 1/ x − 1 − 3) < 0

(если некоторое выражение заключено между двумя числами, то разности между ним и каждым из этих чисел имеют разные знаки).

После выполнения действий в скобках и небольших упрощений получим

x − 2/ ( x − 1)²> 0,

откуда x > 2.

Ответ. x > 2.

10.45.Если 0 < x ² − 1 < 1, то придем к системе

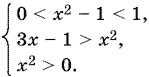
Так как последнее неравенство следует из первого, то получаем такую систему:

откуда 1 < x < √2.

Если x ² − 1 > 1, т. е. x ² > 2, то приходим ко второй системе:

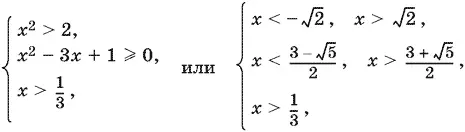
откуда x > 3 + √5/ 2.

Ответ.1 < x < √2, x > 3 + √5/ 2.

10.46.Перепишем неравенство в виде

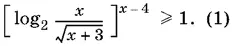
Равносильность при этом не нарушается, так как оба выражения в квадратных скобках (полученное и данное в условии) существуют одновременно при x > 0. Выясним, когда основание положительно и когда оно отрицательно (если оно равно нулю, то неравенство не удовлетворяется). Для этого воспользуемся условным символом V, обозначающим сравнение левой и правой частей, и не будем нарушать равносильность при преобразованиях:

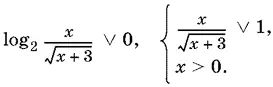
Преобразуем первое соотношение, имея в виду, что x − положительное число:

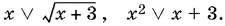
Итак, при 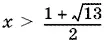основание положительно, а при 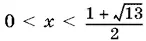оно отрицательно. Из отрицательных значений основания мы должны рассмотреть лишь те, при которых x − 4, а следовательно и x , — четное число. Среди чисел, заключенных в интервале 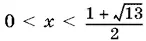, есть только одно четное: x = 2. Подставим это число в левую часть исходного неравенства:

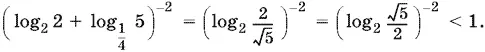
Таким образом, x = 2 не удовлетворяет данному неравенству.

Пусть теперь основание положительно, т. е. 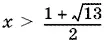. Тогда неравенство (1) равносильно такому: