Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

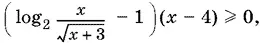
т. е.

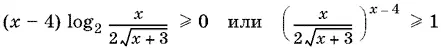
(пояснения приведены во втором указании на с. 192). В последнем неравенстве основание степени положительно, так как x > 0. Следовательно, его можно преобразовать к виду

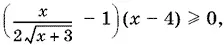
т. е.

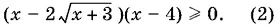
Мы рассматриваем случай 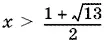. Решив неравенства

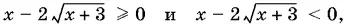
получим, что выражение 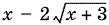больше нуля, когда x > 6, равно нулю, когда x = 6, и меньше нуля, когда 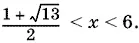Таким образом, вместо неравенства (2) можно записать

( x − 6)( x − 4) ≥ 0,

т. е.

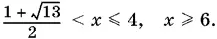
Ответ.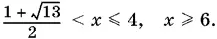

10.47.Данное неравенство может выполняться только в том случае, если дискриминант стоящего в левой части квадратного трехчлена относительно x положителен, т. е.

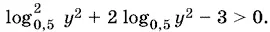
Решением этого неравенства будут

log 0,5 y ² < −3, log 0,5 y ² > 1.

В первом случае получим y ² > 8, во втором 0 < y ² < ½.

Ответ. y < −√8, − 1/ √2< y < 0, 0 < y < 1/ √2, y > √8.

10.48.Для ответа на вопрос задачи нужно найти такие значения а , что множество решений второго неравенства не у́ же множества решений первого. Таким образом, если y первого неравенства есть решения, они все должны попасть в интервал (−3, −1).

Корнями квадратного трехчлена

х ² − а (1 + а ²) x + а 4

будут числа а и а ³. Когда они совпадают ( а = ±1, а = 0), ветви параболы направлены вверх и квадратный трехчлен не может стать отрицательным.

Докажем, что следствием неравенства, не имеющего решений, является любое неравенство. В частности, любое решение первого неравенства при а = 0, ±1 содержится среди решений второго. Предположим, что это не так. Тогда существует решение первого неравенства, не удовлетворяющее второму. Мы приходим к противоречию с тем фактом, что первое неравенство в рассматриваемых случаях вообще не имеет решений.

Если же корни различны ( а ≠ а ³), то оба они должны попасть в интервал [−3, −1]

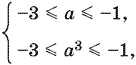
т. е.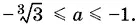

Ответ.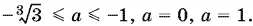

10.49.Сначала решим строгое неравенство

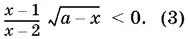
Оно равносильно системе

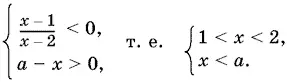
При а ≤ 1 решений y этой системы нет. При а > 1 ее решениями будут значения x , для которых 1 < x < а .

Остается выяснить, какие значения x удовлетворяют уравнению

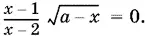
(4)

Это уравнение равносильно совокупности двух систем:

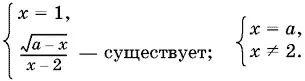
Поскольку в первой системе x = 1, то x ≠ 2; остается обеспечить, чтобы а − 1 ≥ 0, т. е. а ≥ 1.

Итак, при каждом а ≥ 1 есть решение x = 1, а при каждом x ≠ 2 есть решение x = а . (При а = 1 эти решения совпадают.)

Решение второй системы при а ≠ 2: x = а . Остается объединить решения неравенства (3) и уравнения (4).

Ответ.При а ≤ 1 имеем x = а; при 1 < а < 2 имеем 1 ≤ x ≤ а ; при а = 2 имеем 1 ≤ x < 2; при а > 2 имеем 1 ≤ x ≤ 2, x = а .

10.50.Поскольку

х ² + 8 х + 15 = ( x + 3)( x + 5), а x ² + 7 х + 10 = ( x + 2) ( x + 5),

то данное неравенство можно записать в виде

( x + 5)[( x + 3) · 2 2 + x − (2 + x )] > 0. (5)

При x + 5 = 0 исходное неравенство не удовлетворяется. Поэтому (5) равносильно совокупности двух систем:

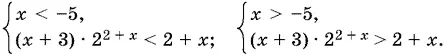
Далее придется рассмотреть случаи x + 3 < 0 и x + 3 > 0 (при x + 3 = 0 неравенство (3) удовлетворяется!). Располагая точки x = −5 и x = −3 на числовой оси, мы получим три интервала x < −5; −5 < x < −3; x > −3. Соответственно, приходим к совокупности трех систем неравенств:

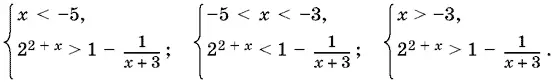
Построим графики функций

y 1= 2 2 + x , y 2= 1 − 1/ x + 3

(рис. P.10.50).

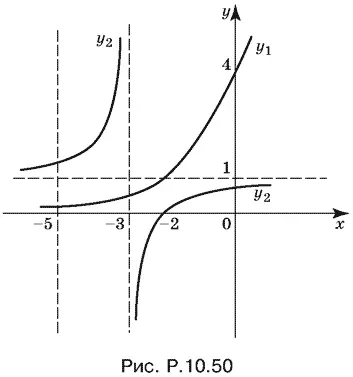
Просто сослаться на график и указать интервалы решений нельзя. График подскажет, какие сравнения нужно привести для решения неравенства.

При всех x < −5 получим, что y 2> 1, а y 1< 1, т. е. y 1< y 2: второму неравенству первой системы значения x < −5 не удовлетворяют.

При −5 < x < −3 также y 1< 1, а y 2> 1 и снова y 1< y 2. Однако на этот раз второе неравенство второй системы удовлетворяется.

При x > −3 второе неравенство третьей системы вновь удовлетворяется. В самом деле, при −3 < x < −2, y 1> 0, а y 2< 0, т. е. y 1> y 2. Далее при x ≥ −2 имеем у 1 ≥ 1, 0 < y 2< 1, т. е. снова у 1> y 2. Остается вспомнить, что x = −3 было решением (5).