Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

откуда

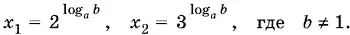
Ответ.При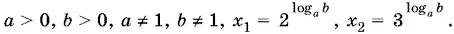

11.19.Логарифмируя и заменяя log xа на 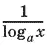, получим

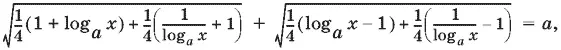
т. е.

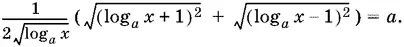
Отсюда видно, что если x удовлетворяет этому уравнению, то log ax > 0, а потому log ax + 1 > 0. Следовательно,

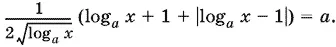
Чтобы разбирать меньшее количество различных случаев, оценим левую часть последнего уравнения и, следовательно, а. Так как

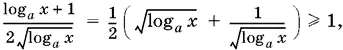
а второе слагаемое неотрицательно, то а > 1 (значение а = 1 мы исключили, так как а — основание логарифма). Остается рассмотреть случаи, позволяющие раскрыть символ абсолютной величины.

При log ax ≥ 1, т. е. при x ≥ а > 1, получим уравнение

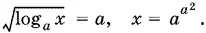
Так как а > 1, то x > а .

При 0 < log ax < 1, т. е. при x < а, получим второе значение неизвестного:

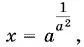
которое будет меньше а , так как а > 1.

Ответ.При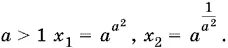

11.20.Если одно из неизвестных равно нулю, то в силу второго уравнения системы равно нулю и второе неизвестное. Это приводит к потере смысла в первом уравнении. Таким образом, x и y оба положительны.

Прологарифмируем оба уравнения:

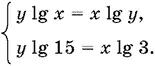
Так как x > 0 и y > 0, то разделим первое уравнение на второе:

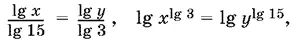
а потому

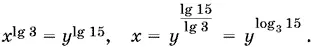
Подставим найденное значение x в первое из данных уравнений:

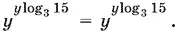
Если y = 1, то из первого уравнения системы получаем x = 1, что не удовлетворяет второму уравнению.

Так как значения y = 0 и y = −1 исключены, то остается

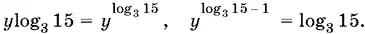
Вспомнив, что log 315 = 1 + log 35, получим

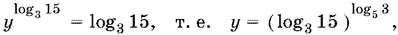
и найдем x .

Ответ.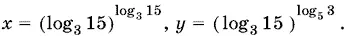

11.21.Возведем второе уравнение в степень y

1024 = ( 2 x / 3) 2 y

и воспользуемся тем, что x y = 243. Так как 1024 = 2 10, а 243 = 3 5, то получим

2 10 = (⅔) 2 y · 3 10, откуда (⅔) 10= (⅔) 2 y

и y = 5. Из первого уравнения находим x = 3.

Делаем проверку и убеждаемся, что мы нашли решение системы.

Ответ.(3, 5).

11.22.Из самого вида системы следует, что x > 0, y > 0. Из второго уравнения имеем

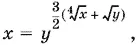
а после подстановки в первое

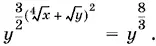
Если y ≠ 1 (случаи y = 0 и y = −1 уже исключены), то, приравнивая показатели степеней, получим

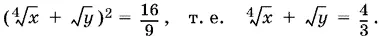
Подставляя в первое уравнение, найдем Следовательно,

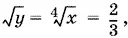
откуда получаем x 1= 16/ 81, у 1= 4/ 9. Проверкой убеждаемся, что это — решение исходной системы.

Остается проверить, что произойдет при y = 1. Легко видеть, что тогда и x = 1.

Ответ.( 16/ 81, 4/ 9), (1, 1).

11.23.Так как

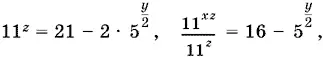
то

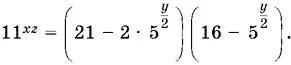
Подставив в первое уравнение исходной системы и обозначив 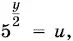получим

(21 − 2 u )(16 − u ) − 2 u ³ = 71,

а после раскрытия скобок

u = 5, т. е. y = 2.

Остальные неизвестные находятся легко.

Ответ.(2, 2, 1).

11.24.Второе уравнение можно записать в виде

2 x + 2 у ( x · 2 x − y + 1+ 3 y · 2 2 x + y ) = 1.

В силу первого уравнения системы выражение в скобках равно 2. Поэтому

2 x + 2 у + 1= 1,

откуда

x + 2 y + 1 = 0, т. е. x = −2 y − 1.

После подстановки в первое уравнение системы получим

2 −3 y − 3= 1/ −4 − 5 y , или 2 3( y + 1)= −(4 + 5 y ).

Чтобы это уравнение имело решение, необходимо выполнение неравенства

−(4 + 5 у ) > 0, т. е. y < − 4/ 5.

Рассмотрим следующие три случая.

1. 3( y + 1) < 0, т. е. y < −1. В этом случае правая часть уравнения должна быть меньше единицы, т. е. −(4 + 5 у ) < 1, откуда y > −1. Поскольку ограничения y < −1 и y > −1 несовместны, при сделанном предположении нет решений.

2. 3( y + 1) > 0, т. е. y > −1. Тогда правая часть уравнения должна превзойти единицу, а потому y < −1. И на этот раз ограничения несовместны.

3. Остается посмотреть, что будет при 3( y + 1) = 0, т. е. y = −1. Легко проверить, что уравнение удовлетворяется. Найденному значению y соответствует x = 1. Проверкой убеждаемся, что мы нашли решение исходной системы.