Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

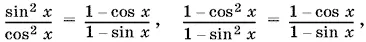
или

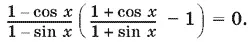
Последнее уравнение равносильно системе

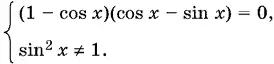
Решая уравнение этой системы, найдем

cos x = 1, откуда x = 2 k π,

cos x = sin x , tg x = 1, откуда x = π/ 4+ k π.

Так как при x = 2 k π и x = π/ 4+ k π условие sin² x ≠ 1 выполняется, то найденные значения x являются корнями данного уравнения.

Ответ. x = 2 k π; x = π/ 4+ k π.

13.3.Поскольку

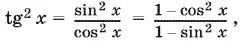
мы приходим к уравнению

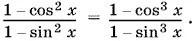
Левая и правая части этого уравнения содержат общий множитель 1 − cos x / 1 − sin x . Поэтому уравнение можно записать в виде

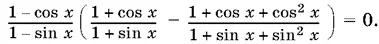
Первые корни получаем из уравнения cos x = 1, откуда x = 2 k π.

Остальные корни найдем, приведя к общему знаменателю дроби, стоящие в скобке, и выполнив вычитание. Получим уравнение

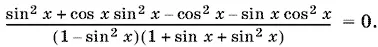
Числитель легко разложить на множители, если сгруппировать однородные члены:

(sin² x − cos² x ) + sin x cos x (sin x − cos x ) = (sin x − cos x )(sin x + sin x cos x + cos x ).

Знаменатель можно отбросить, так как при cos x = 0 ни одна из скобок в разложении числителя не обращается в нуль. Заботиться о том, чтобы 1 + sin x + sin² x не обращалось в нуль, не нужно, так как это выражение всегда положительно.

Если sin x − cos x = 0, то tg x = 1, откуда x = π/ 4+ k π.

Остается решить уравнение

sin x + sin x cos x + cos x = 0.

Мы знаем, что (sin x + cos x )² = 1 + 2 sin x cos x . Отсюда

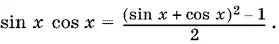
Сделав такую замену в оставшемся уравнении, получим квадратное уравнение относительно y = sin x + cos x

y ² + 2 y − 1 = 0.

Корни этого уравнения

y 1,2 = −1 ± √2.

Записав sin x + cos x в виде √2 cos ( x − π/ 4), мы убедимся, что корень y 1= −1 − √2 является посторонним. Остается

cos ( x − π/ 4) = 1 − 1/ √2,

откуда

x = 2 k π ± arccos (1 − 1/ √2) + π/ 4.

Ответ.2 k π; π/ 4+ k π; 2 k π ± arccos (1 − 1/ √2) + π/ 4.

13.4.Данное уравнение эквивалентно системе

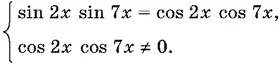
Преобразуя левую и правую части уравнения в сумму тригонометрических функций, мы получим уравнение

cos 9 x = 0, откуда x = π/ 18(2 n + 1).

Из найденных значений x нужно выбрать те, при которых

cos 2 x cos 7 x ≠ 0, т. е. cos 5 x + cos 9 x ≠ 0.

Так как речь идет о значениях неизвестного, при которых cos 9 x = 0, то остается потребовать, чтобы cos 5 x ≠ 0, т. е. 5 · π/ 18(2 n + 1) ≠ π/ 2(2 k + 1), откуда 5(2 n + 1)/ 9≠ 2 k + 1. Число 5(2 n + 1)/ 9 не может быть четным, так как в его числителе лишь нечетные множители.

Оно будет целым, когда = 2 n + 1/ 9= 2 n + 1, т. е. при n = 9 m + 4.

Следовательно, корнями уравнения являются числа x = π/ 18(2 n + 1) при n ≠ 9 m + 4.

Ответ. π/ 18(2 m ± 1); π/ 18(18 m ± 3); π/ 18(18 m ± 5); π/ 18(18 m ± 7).

13.5.Если запишем данное уравнение в виде

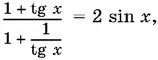
то получим равносильное уравнение. Однако дальнейшие преобразования заставляют нас ввести ограничения:

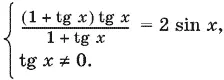
Далее

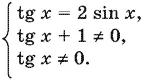
Когда tg x ≠ 0, то и sin x ≠ 0. Это означает, что первое уравнение можно переписать в виде 1/ cos x = 2, откуда cos x = ½, что обеспечивает выполнение всех ограничений.

Ответ.2 n π ± π/ 3.

13.6.Прибавив к обеим частям уравнения tg 3 x , получим

3(tg 3 x − tg 2 x ) = tg 3 x (1 + tg² 2 x ),

или

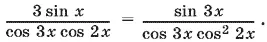
Последнее уравнение эквивалентно системе

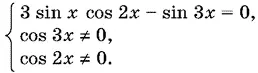
Решим первое уравнение. Для этого представим произведение sin x cos 2x в виде разности синусов. После приведения подобных членов получим

sin 3 x = 3 sin x .

Воспользовавшись формулой синуса тройного угла, придем к уравнению

sin x (3 − 4 sin² x ) = 3 sin x , или sin³ x = 0,

откуда x = π k .

Легко проверить, что при x = π k ни cos 2 x , ни cos 3 x в нуль не обращаются.

Ответ.π k .

13.7.Преобразуем уравнение следующим образом:

(sin x + cos x )(1 − sin x cos x ) + 1/ √2sin 2 x sin ( x + π/ 4) = sin ( π/ 2− x ) + sin 3 x .

Так как sin x + cos x = √2 sin ( π/ 4+ x ), то придем к уравнению

sin ( π/ 4+ x ) = √2 sin ( π/ 4+ x ) cos ( π/ 4− 2 x ).

Если sin ( π/ 4+ x ) = 0, то x 1= π/ 4(4 n − 1). Остается

√2 cos ( π/ 4− 2 x ) = 1,

откуда

x 2= n π, x 3= π/ 4(4 n + 1).

Серии чисел x 1, = π/ 4(4 n − 1) и x 3= π/ 4(4 n + 1) можно объединить: x 1= π/ 4(2 n + 1).

Ответ. π/ 4(2 n + 1); n π.

13.8.Перепишем уравнение следующим образом:

4(tg 4 x − tg 3 x ) = tg 2 x (1 + tg 3 x tg 4 x ).

Приведем выражения в скобках к виду, удобному для логарифмирования:

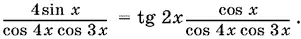
Уравнение равносильно системе

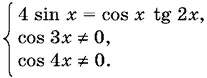
Так как cos x = 0 не удовлетворяет уравнению, то его можно переписать так:

4 tg x = tg 2 x , или 2 tg x = tg x / 1 − tg² x .

Мы воспользовались неабсолютным тождеством, которое исключает из области определения те значения x , при которых tg x не существует. Однако tg x входил в предыдущее уравнение, а потому существует, и потеря корней произойти не может. Из последнего уравнения, если tg x = 0, получаем x = n π.