Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.±arccos(−¼) + k π.

13.15.Данное уравнение равносильно системе

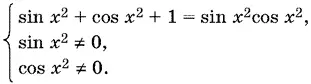
Пусть sin x ² + cos x ² = y . Возведем это соотношение в квадрат: 1 + 2 sin x ² cos x ² = y ², откуда

sin x ² cos x ² = y ² − 1/ 2.

После подстановки и простых преобразований уравнение примет вид

y ² − 2 y − 3 = 0,

откуда y 1= −1, y 2= 3. Второй корень посторонний, так как sin x ² + cos х ² всегда меньше двух.

Если sin x ² + cos x ² = −1, то

cos ( х ² − π/ 4) = − 1/ √2и x ² = 2 n π ± 3π/ 4 + π/ 4.

Взяв знак плюс, получим x ² = π(2 n + 1). Этот корень посторонний, так как sin x ² ≠ 0.

Для знака минус получим, что x ² = − π/ 2+ 2 n π. Это тоже посторонний корень, так как cos x ² ≠ 0.

Ответ.Нет решений.

13.16.Данное уравнение равносильно системе

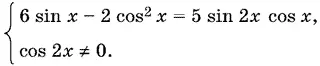
Уравнение можно привести к однородному, домножив 6 sin x на sin² x + cos² x :

3 sin³ x − cos³ x − 2 sin x cos² x = 0.

Обозначим tg x через y , получим

3 y ³ − 2 y − 1 = 0, или ( y − 1)(3 y ² + 3 y + 1) = 0,

где квадратный трехчлен не имеет действительных корней.

Остается y = 1, т. е. tg x = 1, x = π/ 4 + n π. Однако cos 2 x при x = π/ 4+ n π обращается в нуль.

Ответ.Нет решений.

13.17.С помощью формул универсальной подстановки придем к уравнению относительно y = tg x / 2:

y (2 y ³ − 7 у ² − 2 y + 1) = 0.

В результате такой замены могли быть потеряны корни, так как tg x / 2теряет смысл при x = π(2 k + 1), в то время как sin x , cos x и tg x при этих значениях x имеют смысл. Проверкой убеждаемся, что эти значения неизвестного не являются корнями исходного уравнения.

Один корень полученного алгебраического уравнения очевиден: y = 0. Второй мы найдем на основании теоремы о рациональных корнях многочлена, испытав y = ±1; ±½. Убеждаемся, что y = −½ — второй корень уравнения. Разделив многочлен 2 y ³ − 7 у ² − 2 y + 1 на 2 y + 1, получим уравнение

y ² − 4 y + 1 = 0,

которое даст еще два корня: y = 2 + √3, y = 2 − √3.

Если tg x / 2= 2 + √3, то

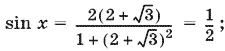
то же самое мы получим и при tg x / 2= 2 − √3.

Так как и обратно из sin x = ½ следует, что

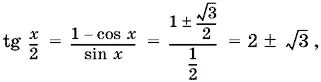
то совокупность уравнений tg x / 2 = 2 + √3 равносильна уравнению sin x = ½. Получаем x = k π + (−1) k π/ 6.

Ответ.2π k ; k π + (−1) k π/ 6; 2π k − 2 arctg ½.

13.18.Понижением степени данное уравнение приводится к виду

2 cos x = 1 + cos 3 x / 2.

С помощью формул для косинуса двойного и тройного углов приходим к уравнению относительно y = cos x / 2:

4 y ³ − y ² − 3 y + 3 = 0.

Левую часть легко разложить на множители:

4 у ²( y − 1) − 3( y − 1) = 0, ( y − 1)(4 у ² − 3) = 0.

Если cos x / 2= 1, то x 1, = 4π n . Если 4 cos² x / 2 = 3, то cos x = ½ и x 2= 2π n ± π/ 3.

Ответ.4π n ; 2π n ± π/ 3.

13.19.Преобразуем выражение, стоящее в квадратных скобках:

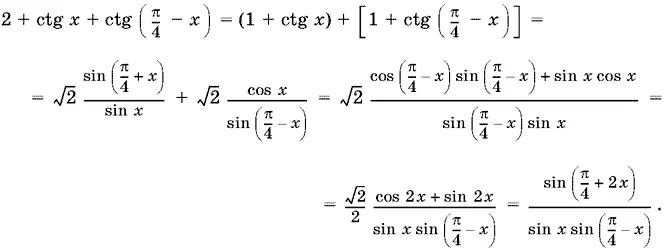
Теперь придем к виду, удобному для логарифмирования, правую часть уравнения:

2√2(1 + sin 2 x + cos 2 x ) = 4√2 cos x (sin x + cos x ) = 8 cos x sin ( π/ 4+ x ). В итоге получаем уравнение

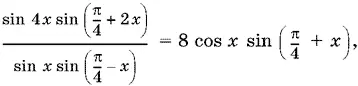
которое равносильно системе

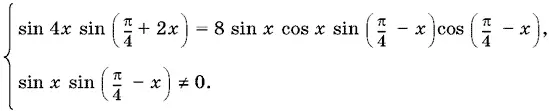
Условие sin x sin ( π/ 4 − x ) ≠ 0 подсказывает, что удобнее в левой части уравнения заменить sin 4 x на его разложение, стоящее справа, чем наоборот. Сокращая после этого обе части уравнения на 8 sin x sin ( π/ 4 − x ) ≠ 0, получим уравнение

cos x cos ( π/ 4 − x )[sin ( π/ 4+ 2 x ) − 1] = 0.

Среди корней уравнений cos x = 0 и cos ( π/ 4 − x ) = 0 не может быть таких, при которых sin x sin ( π/ 4− x ) = 0. Остается проверить корни уравнения sin ( π/ 4 + 2 x ) = 1. Преобразуем вначале условие, которому они должны удовлетворять: sin x sin ( π/ 4− x ) ≠ 0, или cos ( π/ 4− 2 x ) − cos π/ 4 ≠ 0, т. е. cos ( π/ 4− 2 x ) ≠ 1/ √2, или sin ( π/ 4 + 2 x ) ≠ 1/ √2. Теперь ясно, что в уравнение sin ( π/ 4+ 2 x ) = 1 не попали посторонние корни.

Ответ. π/ 2 + n π; − π/ 4+ n π; π/ 8+ n π.

13.20.Перепишем данное уравнение в виде

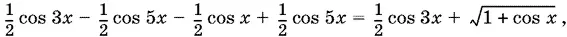
т. е.

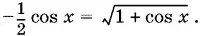
После возведения в квадрат (при этом могут появиться посторонние корни, для которых cos x > 0) получим квадратное уравнение относительно y = cos x:

y ² − 4 у − 4 = 0, т. е. y 1,2 = 2 ± 2 √2.

Положительный корень заведомо посторонний. Остается

cos x = 2 − 2 √2.

Ответ. x = π(2 n + 1) ± arccos |2( √2 − 1)|.

13.21.Так как sin 4 x = 4 sin x cos x (2 cos² x − 1), то данное уравнение можно переписать в виде

sin x [4 cos x (2cos² x − 1) − m / cos x ] = 0.

Если sin x = 0, то x = k π. Это — корни данного уравнения, поскольку cos k π ≠ 0.

Если выражение в квадратных скобках равно нулю, то приходим к биквадратному уравнению

8 cos 4 x − 4 cos² x − m = 0,

среди корней которого не должно быть cos x = 0.

Решая это биквадратное уравнение, получим

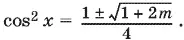
Так как m > 0, то перед корнем берем знак плюс. (Очевидно, что при этом cos x ≠ 0). Воспользуемся формулой

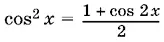
и преобразуем уравнение к виду

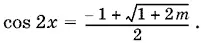
Правая часть этого уравнения положительна. Поэтому, чтобы уравнение имело решение, достаточно

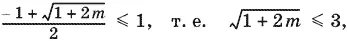
откуда m ≤ 4.