Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

sin пх ≤ n |sin x |,

причем равенство достигается лишь при x = k π. Следовательно, уравнение 7 sin x = sin 7 х имеет решения x = k π.

При этом cos 3 x ≠ 0 и cos 4 x ≠ 0.

Подставляя в выражение для y , получим y = n π.

Ответ. x = k π, y = k π.

13.33.Возведем каждое уравнение в квадрат и сложим:

2 = sin² y + 5 cos² y ,

откуда cos² y = ¼, т. е. cos y = ±½.

Учитывая второе уравнение исходной системы, приходим к совокупности двух систем

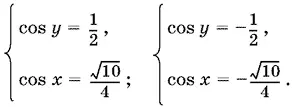
Возводя при решении оба уравнения в квадрат, мы могли приобрести посторонние решения. Отсеять их можно просто: достаточно выбрать sin x и sin y так, чтобы они имели одинаковый знак (для cos x и cos y мы это уже обеспечили). Оба этих требования означают, что x и y должны лежать в одной четверти.

Решая первую систему, получим

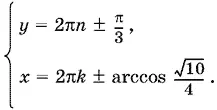
Значения x и y будут лежать в одной четверти, если мы одновременно возьмем только верхние или только нижние знаки.

Аналогично поступаем со второй системой.

Ответ.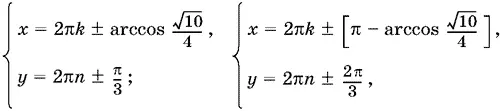

где одновременно берут либо только верхние, либо только нижние знаки.

13.34.Так как sin π x ²/ 2= 1, то

π x ²/ 2 = π/ 2+ 2π n ,

откуда x ² = 4 n + 1 и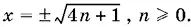

Подставив во второе уравнение, найдем

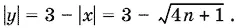
Чтобы это равенство выполнялось, необходимо

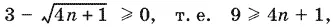
откуда n ≤ 2.

Ответ.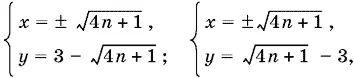

где n = 0, 1, 2. Всего 12 решений (10 не совпадающих).

13.35.Разделив второе уравнение на первое, получим tg y = 2 tg x . Так как x + y = π − z , то tg z = −tg (π − z ) = −tg ( x + y ).

По формуле тангенса суммы получаем

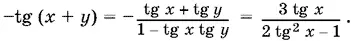
Применение неабсолютного тождества не приводит к потере решений, так как tg x и tg y входят в данную систему.

Подставляем в первое уравнение

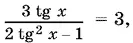
откуда tg² x = 1, x = k π ± π/ 4. Найти y и z теперь не составляет труда.

Производя вычисления отдельно для x = k π + / 4и для x = k π − / 4, после проверки получим решение системы.

Ответ.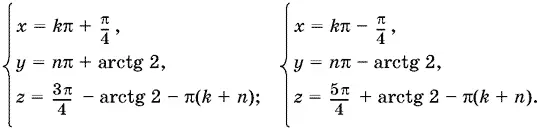

13.36.Так как в уравнения системы входят одновременно tg x и ctg x , tg y и ctg y , то неизвестные не могут принимать значения k π/ 2. С учетом этого данную систему можно записать сначала так:

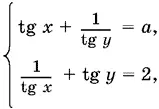
а затем так:

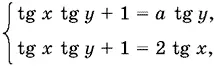
откуда а tg y = 2 tg x .

Если а = 0, то tg x = 0, а ctg x не существует. Поэтому а ≠ 0 и tg y = 2/ a tg x . Подставляем в первое уравнение системы

tg x + a / 2 tg x = a , т. е. 2 tg² x − 2 a tg x + a = 0.

Решаем последнее уравнение:

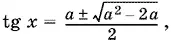
и находим tg y :

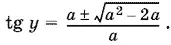
Дискриминант стоящего слева квадратного трехчлена равен а ² − 2 a . Он неотрицателен, если а ≤ 0 или а ≥ 2. Значение а = 0 нужно исключить.

При остальных а ни tg x , ни tg y не обращаются в нуль и существуют. Остается сделать проверку.

Ответ.Если а < 0 или а ≥ 2, то

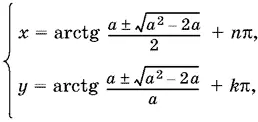
где одновременно берутся либо верхние, либо нижние знаки.

13.37.Перенесем sin y и cos y в правую часть:

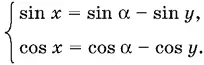
Возведем каждое уравнение в квадрат и сложим:

1 = 2 − 2(sin α sin y + cos α cos y ),

т. е. cos ( y − α) = ½. Таким образом, y − α = 2 n π ± π/ 3. Аналогично найдем x − α = 2 k π ± π/ 3.

Система еще не решена, так как при возведении в квадрат могли быть приобретены посторонние корни. Чтобы сделать проверку, подставим x = α + 2 k π ± π/ 3и y = α + 2 n π ± π/ 3в данную систему:

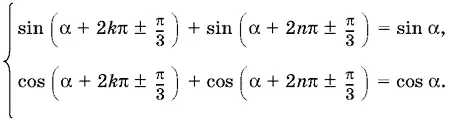
Обратим внимание на то, что в этой записи не исключается возможность выбора произвольных комбинаций знаков плюс и минус для x и y .

Если в выражениях для x и y взять одинаковые знаки, например плюс, то получим систему

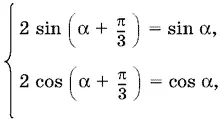
откуда следует

tg (α + π/ 3) = tg α или ctg (α + π/ 3) = ctg α,

что неверно при всех α.

Если взять разные знаки, то

sin (α + π/ 3) + sin (α − π/ 3) = 2 sin α cos π/ 3= sin α,

cos (α + π/ 3) + cos (α − π/ 3) = 2 cos α cos π/ 3= cos α,

т. е. каждое уравнение системы превращается в тождество.

Ответ.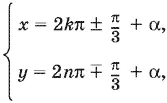

где берутся или только верхние, или только нижние знаки.

Замечание.Найдя y = α + 2 n π ± π/ 3, можно было искать x с помощью подстановки. Однако это не избавило бы нас от необходимости делать проверку, так как в процессе решения уравнения возводились в квадрат.

13.38.Первое уравнение перепишем в виде

sin (x − y ) − cos (x + y ) = 2a.

Из второго найдем

cos ( x + y ) = cos [2 arcsin ( a + ½)] = 1 − 2 sin² [arcsin ( a + ½)] = 1 − 2( a + ½)² = ½ − 2 a ² − 2 a .