Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

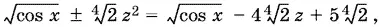
т. е.

± z ² + 4 z − 5 = 0. (7)

Решая каждое из квадратных уравнений (7), найдем два действительных корня: z 1= −5, z 2= 1. Из них подходит только 2 = 1. Следовательно,

cos ( x − π/ 4) = 1, откуда x = π/ 4+ 2 n π.

Остается сделать проверку, которая осуществляется непосредственной подстановкой в исходное уравнение.

Ответ. x = π/ 4+ 2 n π.

13.47.Система уравнений может быть переписана так:

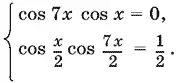
Если cos x = 0, то x = (2 k + 1) π/ 2и, следовательно, cos 7 x = 0. Поэтому первое уравнение равносильно уравнению cos 7 x = 0, т. е.

2 cos² 7 x / 2= 1 и cos² 7 x / 2= ½.

Возведя второе уравнение системы в квадрат, получим теперь, что одновременно и cos² x / 2= ½. Таким образом, исходная система уравнений равносильна совокупности двух систем

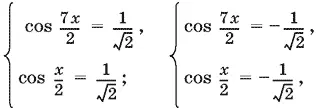
в которых множество решений вторых уравнений входит в множество решений первых. (Докажите.) Это означает, что система сводится к совокупности двух вторых уравнений

cos x / 2= ± 1/ √2, т. е. cos² x / 2= ½,

откуда cos x = 0 и x = (2 k + 1) π/ 2. Из найденной серии чисел отбираем те, которые удовлетворяют ограничению | x | < 5.

Ответ. x = ± π/ 2, ± 3π/ 2.

13.48.Преобразуем левую часть уравнения, пользуясь тем, что tg x = sin x / cos x , tg² x = 1/ cos² x − 1, а cos x ≠ 0:

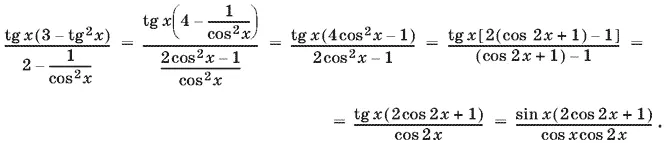
Для правой части уравнения получим

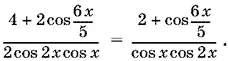
При cos x ≠ 0 и дополнительном ограничении cos 2 x ≠ 0 приведем исходное уравнение к виду

2 sin x cos 2 x + sin x = 2 + cos 6 x / 5.

Произведение 2 sin x cos 2 x преобразуем в разность синусов. Тогда в левой части останется только sin 3 x (так как 2sin x cos 2 x = sin 3 x − sin x ) и уравнение примет вид

sin 3 x = cos 6 x / 5+ 2.

Такое возможно лишь при условии, что одновременно

cos 6 x / 5 = −1, а sin 3 x = 1.

Поэтому данное в условии уравнение равносильно системе:

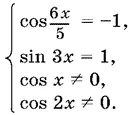
Не следует решать каждое из уравнений и отдельно записывать для них общие ограничения. Это не приведет к результату. Лучше начать с первого уравнения — его корни имеют простую запись, а затем отсеивать из решений первого уравнения те, что не удовлетворяют остальным требованиям. Итак, из уравнения cos 6 x / 5= −1 найдем, что

6 x / 5= π(2 k + 1), т. е. x = 5(2 k + 1) π/ 6.

Проверим, чему равняется при найденных x значение sin 3 x . Поскольку

3 x = 5(2 k + 1) π/ 2= 5π k + 5 π/ 2,

то найти sin 3 x мы сможем, рассмотрев две возможности: k = 2 n , k = 2 n + 1.

При k = 2 n , т. е. k — четном

3 x = 10π n + 5 π/ 2= 10π n + 2π + π/ 2.

Мы выделили период и поэтому sin 3 x при k = 2 n равняется sin π/ 2= 1, т. е. второе уравнение системы удовлетворяется. Если же k = 2 n + 1, т. е. k — нечетное, то

3 x = 5π(2 n + 1) + 5 π/ 2= 10π n + 5π + 2π + π/ 2= 10π n + 4π + π + π/ 2,

т. е. sin 3 x = −1. На этот раз второе уравнение системы не удовлетворяется.

Обоим уравнениям удовлетворяют значения x = 5(4 n + 1) π/ 6. (Мы просто подставили k = 2 n в найденное выше выражение для x .)

Перейдем к ограничению cos x ≠ 0. Преобразуем выражение для x :

x = 20 π n / 6+ 5 π/ 6= 10 π n / 3+ 5 π/ 6.

Чтобы при разных n вычислить cos x , нужно рассмотреть случаи n = 3 m , n = 3 m + 1, n = 3 m − 1. (Обратите внимание, что вместо n = 3 m − 1 можно рассматривать n = 3 m + 2, но n = 3 m − 1 удобнее.)

Для n = 3 m получим

x = 10π m + 5 π/ 6, cos x = cos 5π/ 6≠ 0;

при n = 3 m + 1:

x = 10π 3 m + 1/ 3+ 5 π/ 6= 10π m + 10 π/ 3+ 5 π/ 6= 10π m + 25 π/ 6= 10π 0 + 4π + π/ 6,

т. е. cos x = cos π/ 6 ≠ 0,

при n = 3 m − 1:

x = 10π 3 m − 1/ 3+ 5 π/ 6= 10π m − 10 π/ 3+ 5 π/ 6= 10π m − 15 π/ 6= 10π m − 2π − π/ 2,

т. е. cos x = cos (− π/ 2) = 0.

Итак, значение n = 3 m − 1 не подходит, а при остальных n ограничение cos x ≠ 0 удовлетворяется.

Остаются два варианта:

x = 5(12 m + 1) π/ 6, x = 5(12 m + 5) π/ 6, m = 0, ±1, ±2.

Непосредственной подстановкой убеждаемся, что cos 2 x ≠ 0 для каждого из найденных значений.

Ответ.5(12 m + 1) π/ 6; 5(12 m + 5) π/ 6.

13.49.Обе части уравнения существуют, если cos x ≠ 0, sin 2 x ≠ 0, cos 2 x ≠ 0.

Все эти ограничения равносильны условию sin 4x ≠ 0, поскольку

sin 4 x = 2 sin 2 x cos 2 x = 4 sin x cos x cos 2 x .

Если sin 4 x ≠ 0, то все последующие преобразования правомерны. Преобразуем левую часть, воспользовавшись соотношениями:

tg² x + 1 = 1/ cos² x , cos 3 x + cos x = 2 cos 2 x cos x .

Тогда

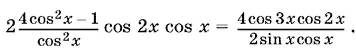
Так как cos 2 x ≠ 0, cos x ≠ 0, то

4 cos² x − 1 = cos 3 x / sin x .

Поскольку 2 cos² x = 1 + cos 2 x и sin x ≠ 0, получим

2 cos 2 x sin x + sin x = cos 3 x ,

или

sin 3 x − sin x + sin x = cos 3 x ,

т. е. tg 3 x = 1, откуда 3 x = π/ 4+ π k = π/ 4(4 k + 1), k = 0, ±1, ±2, или x = π/ 12(4 k + 1).

Теперь нужно позаботиться о соблюдении ограничения sin 4 x ≠ 0, т. е. 4 x ≠ π n , x ≠ π n / 4.

Равенство

π/ 12(4 k + 1) = π n / 4, или π/ 3(4 k + 1) = π n , (8)

может иметь место, когда 4 k + 1 делится на 3. Поэтому рассмотрим три случая: k = 3 m , k = 3 m + 1, k = 3 m − 1. Тогда для 4 k + 1 получим

4(3 m ) + 1 = 12 m + 1,

4(3 m + 1) + 1 = 12 m + 5,

4(3 m − 1) + 1 = 12 m − 3 = 3(4 m − 1).

Последний из вариантов должен быть исключен, так как именно в этом случае равенство (8) имеет место.

Ответ. π/ 12(12 m + 1); π/ 12(12 m + 5).

13.50.Представим уравнение в виде

2(tg x + ctg 2 x ) + (tg x / 2+ ctg 2 x ) + (ctg 2 x − ctg 3 x ) = 0.

Преобразуем

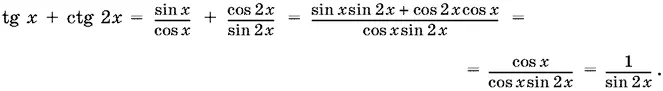
(Сокращение на cos x возможно, так как ограничение cos x ≠ 0 остается благодаря наличию множителя cos x в знаменателе sin 2 x .)

Аналогично

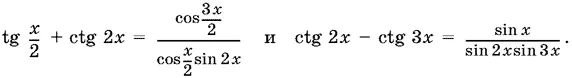
(Во второй дроби sin x − общий множитель числителя и знаменателя. Однако сокращать на него не следует, хотя это и возможно).