Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

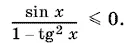
Когда sin x ≥ 0, то получим tg x < −1, tg x > 1 (рис. P.14.5, д ), а когда sin x ≤ 0, то −1 < tg x < 1 (рис. P.14.5, e ). Объединяя все решения на одном чертеже (не забывайте про рис. P.14,5, г ), запишем окончательный ответ (см. рис. P.14.5, в ).

Ответ. π/ 4+ 2 n π < x < 3π/ 4+ 2 n π; π + 2 n π ≤ x < 5π/ 4+ 2 n π; 7π/ 4+ 2 n π < x ≤ 2( n + 1)π; x = (4 n − 1) π/ 2.

14.6.Выразим все тригонометрические функции через cos x = y . Получим неравенство

2 y ² + 13 y + 5 ≥ |2 y ² − 3 y + 1|.

Оно равносильно совокупности систем

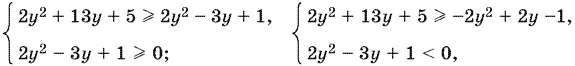
или

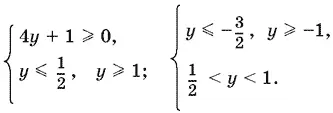
Так как y = cos x , то −1 ≤ y ≤ 1. Учитывая это ограничение, получим

−¼ ≤ y ≤ ½, y = 1, ½ < y < 1,

т. е.

cos x ≥ −¼.

Ответ.π(2 k − 1) + arccos ¼ ≤ x ≤ π(2 k + 1) − arccos ¼.

14.7.Если cos x = 0, то sin² x = 1 и неравенство не удовлетворяется.

Поделим обе части неравенства на cos² x и обозначим tg x = y. Получим алгебраическое неравенство

√2 y ² − 2 y + 2 − √2 < 0.

Разделив на √2, получим неравенство

y ² − √2 y + √2 − 1 < 0,

откуда

√2 − 1 < tg x < 1.

Из интервалов, в которых лежит x :

arctg (√2 − 1) + n π < x < π/ 4+ n π,

выбираем решения, лежащие в (0, 2π).

Ответ.arctg (√2 − 1) < x < π/ 4; π + acrtg (√2 − 1) < x < 5π/ 4.

14.8.Дискриминант трехчлена равен

(2 cos α − 1)² − 4 cos² α + 10 cos α − 4 = 6 cos α − 3.

Чтобы уравнение имело различные действительные корни, нужно потребовать

6 cos α − 3 > 0; т. е. cos α > ½,

откуда 0 ≤ α < π/ 3(в условии сказано, что 0 ≤ α ≤ π).

Свободный член сравним с нулем:

2cos² α − 5cos α + 2 ∨ 0.

Так как корнями трехчлена 2 y ² − 5 у + 2 будут числа ½ и 2, то свободный член будет положителен при cos α < ½ и отрицателен при cos α > ¼. Мы уже выяснили, что должно иметь место второе неравенство; таким образом, исходное уравнение имеет корни разных знаков.

Поскольку x 1+ x 2= 2cos α − 1, что при cos α > ½ больше нуля, то положительный корень имеет большую абсолютную величину.

Ответ.Данное уравнение имеет два различных действительных корня при 0 ≤ α < π/ 3. Эти корни имеют разные знаки, причем положительный корень больше по абсолютной величине.

14.9.Если sin x ≥ 0 и cos x ≥ 0, то данное неравенство равносильно такому:

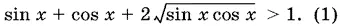
Так как при sin x ≥ 0 и cos x ≥ 0 имеем

sin x + cos x ≥ 1,

а при sin x > 0 и cos x > 0 это неравенство становится строгим, то отсюда следует, что неравенство (1) равносильно системе

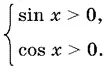
Ответ.2 n π < x < π/ 2+ 2 n π.

14.10.Данное неравенство означает, что

π/ 4+ k π ≤ 1/ 1 + x ²< π/ 2+ k π.

Если k > 0, то левое неравенство не имеет решений, поскольку 1/ 1 + x ² не превосходит единицы. Если k < 0, то не имеет решений правое неравенство, так как 1/ 1 + x ² — величина, положительная при всех x . Остается случай k = 0. При k = 0 правое неравенство удовлетворяется всегда. Решим левое неравенство.

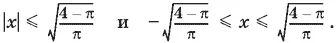
Ответ.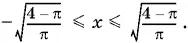

14.11.Так как sin x + cos x = √2 cos ( x − π/ 4), то, обозначив cos ( π/ 4− x ) = y , получим неравенство

Это неравенство равносильно такому:

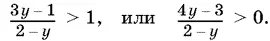
Так как y не превосходит 1, то 2 − y > 0. Поэтому y > ¾.

Решением неравенства cos ( π/ 4− x ) > ¾ будут значения x − π/ 4, лежащие между 2 k π − arccos ¾ < x < 2 k π + arccos ¾.

Ответ.2 k π + π/ 4− arccos ¾ < x < 2 k π + π/ 4 + arccos ¾.

14.12.Перепишем неравенство в виде

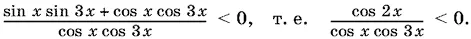
Преобразуем знаменатель

cos x cos 3 x = ½(cos 2 x + cos 4 x ) = ½(cos 2 x + 2 cos² 2 x − 1)

и введем обозначение cos 2 x = y . Получим

откуда y < −1, 0 < y < ½ и, наконец, 0 < cos 2 x < ½.

Ответ:− π/ 4+ n π < x < − π/ 6+ n π; π/ 6+ n π < x < / 4+ n π.

14.13.Пусть y = cos x , где | y | ≤ 1. Выражение 17/ 7− cos x всегда положительно. Поэтому обе части данного неравенства можно возвести в квадрат; получим равносильное неравенство

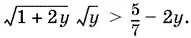
Когда правая часть отрицательна, придем к системе

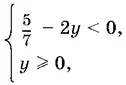
решением которой будут значения y > 5/ 14·

Когда правая часть неотрицательна, то получим другую систему

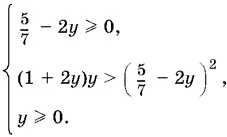
Второе неравенство этой системы можно переписать в виде

2 · 49 у ² − 7 · 27 у + 25 < 0,

откуда

1/ 7< y < 25/ 14, т. е. y > 1/ 7, так как y = cos x .

Решения всей системы будут лежать в интервале

1/ 7< y ≤ 5/ 14

Объединяя его с интервалом y > 5/ 14, получим y > 1/ 7·

Ответ. −arccos 1/ 7+ 2 n π < x < arccos 1/ 7+ 2 n π.

14.14.Выразим sin x и cos x через tg x / 2и обозначим tg x / 2= y . Придем к неравенству

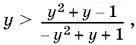
которое равносильно исходному. В самом деле, замена sin x и cos x их выражениями через tg x / 2может привести к потере решений, так как tg x / 2перестает существовать в тех точках, в которых sin x и cos x существуют Однако tg x / 2входит в первоначальное неравенство, а потому эти точки исключены с самого начала. Сокращение числителя и знаменателя на y ² + 1, очевидно, не приводит ни к потере, ни к приобретению корней, так как y ² + 1 ≠ 0 и y не исчез полностью из неравенства.