Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. π/ 4+ k π < x < π/ 2+ k π.

15.3.Так как выражения, стоящие под знаками логарифмов, должны быть положительными, то указанный в условии интервал можно сузить: 0 < x < π/ 2. Данное неравенство равносильно системе

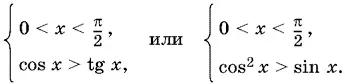
Второе неравенство перепишем в виде

sin² x + sin x − 1 < 0,

откуда

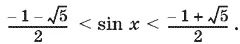
Учитывая, что в интервале 0 < x < π/ 2должно быть sin x > 0, получим

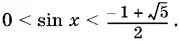
Ответ.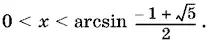

15.4.Данное неравенство можно переписать так:

log 2cos 2 x + log 2sin x + log 2cos x + log 28 < 0,

т. е.

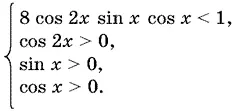
Первое неравенство можно переписать в виде

sin 4 x < ½.

Два последних неравенства требуют, чтобы подвижный радиус угла x лежал в первой четверти, а неравенство cos 2 x > 0 сужает эту область до первой половины первой четверти (на рис. P.15.4, а — заштрихованный сектор).

Остается выбрать решения неравенства sin 4 x < ½, лежащие в этих промежутках. Все решения неравенства sin 4 x < ½ можно записать в виде

− 7π/ 6+ 2 n π < 4 x < π/ 6+ 2 n π,

т. е.

− 7π/ 24+ n π/ 2< x < π/ 24+ n π/ 2

(рис. P.15.4, а ). В интересующий нас интервал 0 < x < π/ 4из этой серии частично попадут лишь два интервала: − 7π/ 24< x < 13π/ 24 (рис. P.15.4, б ). Теперь нетрудно написать окончательный ответ.

Ответ.2 n π < x < π/ 24+ 2 n π; 5π/ 24+ 2 n π < x < π/ 4+ 2 n π.

15.5.Вместо данного неравенства можно написать 0 < |cos x + √3 sin x | < 1, что равносильно системе

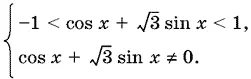
Так как cos x + √3 sin x = 2 cos ( x − π/ 3), то получим

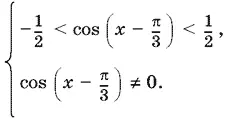
В условии сказано, что 0 ≤ x ≤ 2π, поэтому x − π/ 3нужно искать в интервале − π/ 3 ≤ x − π/ 3≤ 2π − π/ 3.

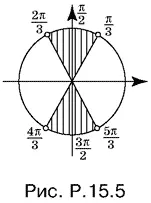
На рис. P.15.5 изображено расположение на тригонометрическом круге значений y = x − π/ 3, удовлетворяющих последней системе, т. е.

π/ 3< x − π/ 3< π/ 2, π/ 2< x − π/ 3< 2π/ 3,

4π/ 3< x − π/ 3< 3π/ 2, 3π/ 2< x − π/ 3< 5π/ 3,

Ответ. 2π/ 3< x < 5π/ 6, 5π/ 6< x < π,

5π/ 3< x < 11π/ 6, 11π/ 6< x < 2π.

15.6.Неравенство можно переписать так:

cos (|lg x | − π/ 4) > ½,

откуда

− π/ 3+ 2 n π < |lg x | − π/ 4< π/ 3+ 2 n π,

т. е.

− π/ 12+ 2 n π < |lg x | < 7π/ 12+ 2 n π.

При n < 0 не удовлетворяется правое неравенство.

При n = 0 имеем |lg x | < 7π/ 12, т. е. − 7π/ 12< lg x < 7π/ 12, а потому

При n = 1, 2, 3, ... имеем − π/ 12+ 2 n π < lg x < 7π/ 12+ 2 n π и − 7π/ 12− 2 n π < lg x < π/ 12− 2 n π.

Ответ. 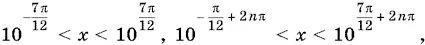n = 1, 2, 3, ... .

15.7.Так как arccos ( х ² + З х + 2) ≥ 0, то данное неравенство равносильно системе

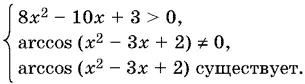
Другими словами,

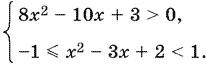
Решаем каждое из трех неравенств системы:

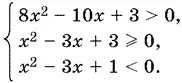
Дискриминант второго неравенства отрицателен, а потому оно удовлетворяется при всех x . Остаются первое и третье:

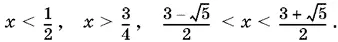
Ответ.

15.8.Если 1 − x ≤ 0, то неравенство не удовлетворяется, так как

arccos (1 − x ) ≥ π/ 2, если 1 − x ≤ 0,

в то время как arctg √ x всегда меньше π/ 2. При 1 − x > 0 обе части неравенства оказываются в интервале от 0 до π/ 2, где все тригонометрические функции монотонны. Так как косинус в интервале от 0 до π/ 2убывает, то данное неравенство равносильно такому:

cos (acrtg √ x ) < cos (arccos (1 − x ))

(большему углу соответствует меньший косинус). Чтобы arccos (1 − x ) существовал, необходимо 1 − x ≤ 1. Вспоминая, что 1 − x > 0, получим 0 ≤ x < 1.

Вычислим cos (arctg √ x ):

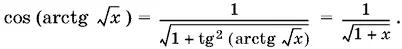
Получаем систему неравенств

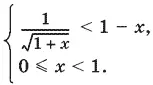
Так как 0 ≤ x < 1, то система равносильна такой:

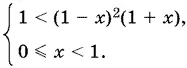
Раскрыв скобки, запишем первое неравенство так: x ³ − x ² − x > 0, или x ( х ² − x − 1) > 0. При x = 0 это неравенство не удовлетворяется, а при x > 0 — равносильно неравенству x ² − x − 1 > 0. Трехчлен, стоящий в левой части, можно записать так: x ( x − 1) − 1. Поскольку x > 0, а x − 1 < 0, то этот трехчлен отрицателен.

Ответ.Нет решений.

15.9.Так как cos² π x + 1 ≥ 1, то второй сомножитель неотрицателен при всех значениях x . Следовательно, неравенство удовлетворяется лишь при положительных значениях сомножителей. Один из них должен быть при этом не меньше единицы. Однако второй не превышает единицы. Для первого же условие 4 x − x ² − 3 ≥ 1 равносильно требованию −( x − 2)² ≤ 0, что возможно лишь при x = 2.

Одновременно должно удовлетворяться неравенство

log 2(cos² π x + 1) ≥ 1,

которому удовлетворяют числа x = n (n = 0, ±1, ±2, ...). Из них выбираем то, которое обеспечивает равенство единице первого сомножителя.