Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

которое требуется решить по условию задачи. Получим

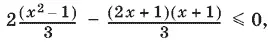
или после простых преобразований:

x + 1 ≥ 0, т. е. x ≥ −1.

Ответ. x ≥ −1.

17.2.Сначала заметим, что

f ( x ) = x ( x ² − 6 x + 9) = x ( x − 3)². (3)

Теперь подставим в (3) вместо x выражение f ( x ):

f ( f ( x )) = f ( x )[ f ( x ) − 3]² = x ( x − 3)²( x ³ − 6 x ² + 9 x − 3)². (4)

Уравнение f ( f ( x )) = 0 имеет корни x 1= 0, x 2= 3, а также корни уравнения

x ³ − 6 x ² + 9 x − 3 = 0. (5)

При всех x ≤ 0 значения (6) отрицательны. При всех x ≥ 4 значения (6) положительны. Поэтому все корни (6) лежат в интервале (0, 4). Найдем корни производной функции (6):

y ′ = 3 x ² − 12 x + 9 = 3( х ² − 4 x + 3) = 3( x − 1)( x − 3).

При x = 1 значение y достигает максимума y = 1, а при x = 3 — минимума −3. Следовательно, функция (6) пересекает по одному разу ось Ox на каждом из интервалов (0, 1), (0, 3), (3, 4), т. е. имеет 3 корня. Таким образом, уравнение (2) имеет 5 различных корней.

Ответ.5.

17.3.Из второго уравнения находим

5π z = π + 2π k , k — целое,

т. е.

z = 1 + 2 k / 5, k — целое.

Подставим в первое уравнение:

5 · 2 x ² − 2 xy + 1= (1 + 2 k )3 y ² − 1. (7)

Если y — целое, то 3 y ² − 1— целое при всех y ≠ 0. Рассмотрим вначале случай y = 0. Тогда уравнение (7) примет вид

5 · 3 · 2 x ² + 1= 2 k + 1,

и целых решений y него нет, поскольку при любых целых x слева — четное число, а справа — нечетное. Итак, y ≠ 0. Так как множителя 3 в левой части (7) нет, то это уравнение удовлетворяется только при y ² = 1. При y = 1 получим

5 · 2 x ² − 2 xy + 1= 2 k + 1, т. е. 5 · 2 ( x −1)²= 2 k + 1.

Левая часть последнего уравнения будет четным числом при всех целых x ≠ 1. Правая часть — нечетное число. Поэтому есть единственная возможность x = 1, а k = 2.

Получим решение: x = 1, y = 1, z = 1.

При y = −1 придем к уравнению

5 · 2 ( x + 1)²= 2 k + 1,

которое удовлетворяется только при x = −1 и k = 2. Находим еще одно решение системы: x = −1, y = −1, z = 1.

Других решений y системы нет.

Ответ.(1, 1, 1), (−1, −1, 1).

17.4.Неравенство

| x + 2| ≤ x + 2

имеет решение x ≥ −2.

Обозначим

2 x − 1= y , sin π x / 2= z . (8)

Тогда уравнение, входящее в систему, примет вид

(4 у + y + 1/ y ) z + (1 − 2 z ²) = 3 + 2 y ²,

а после простых преобразований

2 z ² − (5 у + 1/ y ) z + 2(1 + y ²) = 0. (9)

Дискриминант уравнения (9), квадратного относительно z , равен:

D = (5 у + 1/ y )² − 16(1 + y ²) = 9 у ² − 6 + 1/ y ²= (3 у − 1/ y )².

Поэтому решениями уравнения (9) будут:

z 1= ¼[5 у + 1/ y − (3 y − 1/ y )] = ½( y + 1/ y ), (10)

z 2 = ¼[5 у + 1/ y + (3 у − 1/ y )] = 2 y .

Из (8) следует, что y > 0. Из неравенства, связывающего среднее арифметическое и среднее геометрическое двух положительных чисел, при y > 0 вытекает неравенство: y + 1/ y ≥ 2. Однако z = sin π x / 2, т. е. | z | ≤ 1. Но

z 1= ½( y + 1/ y ).

Поэтому одновременно | z 1| ≤ 1 и z 1 ≥ 1, т. е. имеется единственная возможность z 1= 1, что достигается при y = 1, а следовательно, при x = 1. Подставим значение x = 1 в исходную систему и убедимся, что это ее решение.

Для z 2получим

sin π x / 2= 2 x , где x ≥ −2. (11)

При x > 0 решений уравнение (11) не имеет, поскольку тогда 2 x > 1, а |sin π x / 2| ≤ 1.

Значение x = 0 тоже решением не является, в чем убеждаемся непосредственной проверкой.

Когда −2 ≤ x < 0, решений тоже нет, так как при этих x значения 2 x положительны, а значения sin π x / 2 ≤ 0.

Ответ. x = 1.

17.5.Первообразная F ( x ) для функции f ( x ) = 6 х ² + 2 x + 6 равна:

F ( x ) = 2 x ³ + x ² + 6 х + С , (12)

где константа С будет определена. Соответственно

f ′( x ) = 12 x + 2. (13)

В точке касания x 0> 0,7 должны иметь место следующие соотношения:

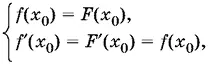
т. е. получаем систему

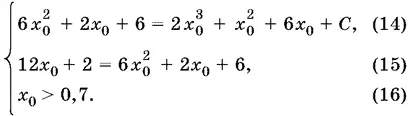
Уравнение (15) после упрощений принимает вид

Из его двух корней x 0= ⅔ и x 0= 1 условию (16) удовлетворяет только второй. Подставляем x 0= 1 в уравнение (14) и находим, что С = 5. Окончательно

F ( x ) = 2 x ³ + x ² + 6 х + 5.

Остается сформировать данное в условии задачи неравенство

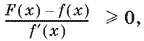
которое примет вид

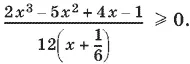
Разложим числитель на множители

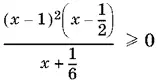
и воспользуемся методом интервалов (рис. P.17.5). Ограничение x > 0,7 относилось только к расположению точки касания графиков f ( x ) и F ( x ). Здесь его учитывать не нужно.

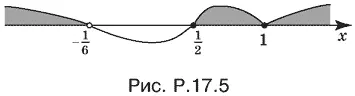
Ответ. x ∈ (−∞; − 1/ 6) ∪ [½; +∞).

17.6.По условию разность x − y такова, что может быть основанием логарифма. Поэтому возможна замена 1 = log x − y ( x − y ), а данное в условии неравенство равносильно такому:

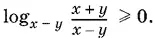
Так как ( x − y ) — основание логарифма, то либо 0 < x − y < 1, либо x − y > 1. Получим совокупность двух систем, которую затем несколько преобразуем, чтобы удобнее было перейти к графическим изображениям:

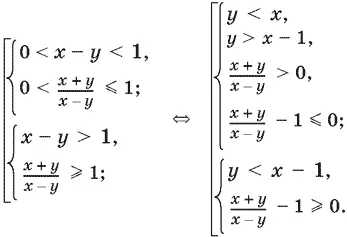
Последние два неравенства первой системы можно упростить, поскольку имеет место условие x − y > 0. Получим

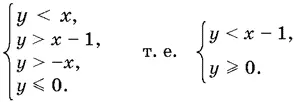
Решение первой системы показано на рис. P.17.6, а , решение второй — на рис. P.17.6, б , а решение совокупности — на рис. P.17.6, в .