Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ. 2 k π + arctg √8; (2 k + 1)π − arctg √8.

16.9.Данное уравнение эквивалентно такому:

(½) x = 4 k + 1/ 20.

Так как x > 0, то (½) x заключено между нулем и единицей. Следовательно, 0 < 4 k + 1/ 20< 1, откуда 0 ≤ k ≤ 4.

Для каждого из этих k находим соответствующее значение x .

Ответ.log 2 20/ 4 k + 1, где k = 0, 1, 2, 3, 4.

16.10.Решаем квадратное уравнение

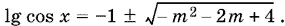
Стоящее под корнем выражение неотрицательно, если −1 − √5 ≤ m ≤ −1 + √5.

Делаем следующий шаг:

Когда перед корнем взят минус, то стоящее справа положительное выражение не превзойдет единицы, а потому может быть косинусом. Когда перед корнем поставлен плюс, нужно, чтобы

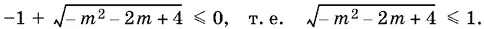
После возведения в квадрат, учитывая полученные вначале ограничения для m , придем к системе

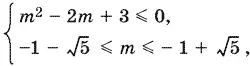
y которой два интервала решений:

−1 − √5 ≤ m ≤ −3, 1 ≤ m ≤ −1 + √5.

Ответ.При −1 − √5 ≤ m ≤ −1 + √5, x = 2 n π ± arccos A ,

при −1 − √5 ≤ m ≤ −3 и 1 ≤ m ≤ −1 + √5, x = 2 n π ± arccos B , где

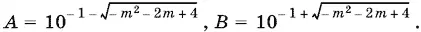
16.11.Решаем квадратное уравнение относительно lg sin x :

Подкоренное выражение должно быть неотрицательным: 2 а ² − 2 ≥ 0, т. е. а ≤ −1, а ≥ 1.

Поскольку

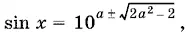
то правая часть не должна превосходить единицу, а потому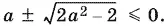

Когда а ≥ 1, нужно рассмотреть лишь неравенство

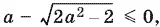
откуда (с учетом ограничения а > 1) получаем а > √2. Если же а ≤ −1, то 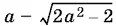всегда отрицательное число, а чтобы и число 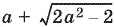было неположительно, должно быть еще а ≥ −√2.

Ответ.При а ≤ −√2

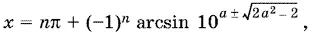
при −√2 ≤ а ≤ −1 и при а ≥ √2

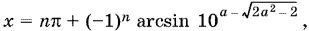
при −1 < а < √2 решений нет.

16.12.Данная система равносильна такой:

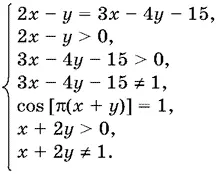
Решая входящие сюда два уравнения, получим

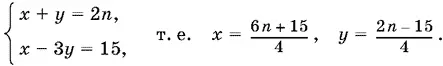
Из первого уравнения большой системы следует, что второе и третье неравенства выполняются одновременно. Поэтому достаточно потребовать

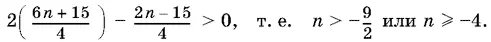
Аналогично убеждаемся, что условие 3 x − 4 у − 15 ≠ 1 выполняется при n ≠ − 41/ 10, т. е. всегда, ибо n — целое.

Неравенство x + 2 y > 0 справедливо при всех n > 1,5, т. е. n ≥ 2, а условие x + 2 y ≠ 1 выполняется при n ≠ 1,9, т. е. всегда.

Ответ.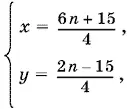

где n = 2, 3, 4, ... .

16.13.Если 4 cos² π x = u , то

4 sin² π x = 4 1 − cos² π x = 4/ u .

Следовательно, левая часть уравнения обращается в 4/ u + u, где u > 0. В силу неравенства, связывающего среднее арифметическое чисел u и 4/ u со средним геометрическим этих же чисел, имеем

4/ u + u ≥ 4.

Для оценки правой части уравнения выделим полный квадрат:

−8 x ² + 12| x | − ½ = −2( 2| x | − 3/ 2)² + 4 ≤ 4.

Поскольку левая часть уравнения не может стать меньше 4, в то время как правая его часть не может превзойти 4, остается проверить те два значения x = ±¾, при которых правая часть достигает своего наибольшего значения. Непосредственной проверкой убеждаемся, что x = ±¾ — корни данного уравнения.

Ответ. x = ±¾.

16.14.Запишем уравнение в виде

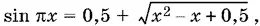
или

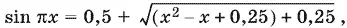
т. е.

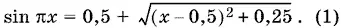
Так как sin π x ≤ 1, а

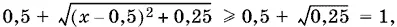
то (1) имеет единственное возможное решение, когда обе части равенства равны 1. Правая часть равна 1 при x = 0,5. Вычислим sin π x при x = 0,5: sin 0,5π = sin π/ 2= 1.

Ответ.0,5.

17.1.Запишем данную систему в виде

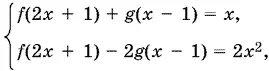
которую решим относительно f (2 x + 1) и g ( x − 1):

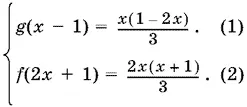
В уравнении (1) осуществим замену переменной: x − 1 = y , т. е. x = y + 1. Тогда

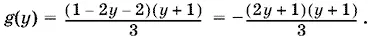
В уравнении (2) сделаем замену: 2 x + 1 = z , т. е. x = z − 1/ 2. Тогда

Теперь мы знаем, что

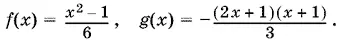
Подставим эти значения в неравенство

4 f ( x ) + g ( x ) ≤ 0,