Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Ответ.При m > 0 уравнение имеет решение x = n π; при 0 < m ≤ 4:

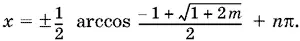
13.22.Раскроем скобки и применим формулу преобразования произведения синусов в разность косинусов:

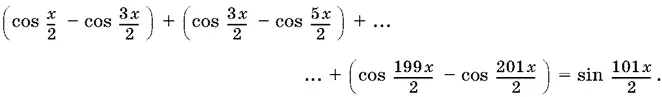
Приведя подобные члены, получим

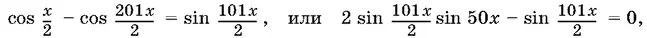
откуда

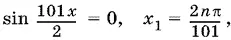
и

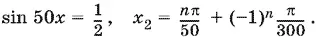
Ответ.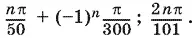

13.23.Так как

sin kх sin k ² x = 1 {cos [( k − 1) kx ] − cos [ k ( k + 1) x ]}, то уравнение можно переписать в виде

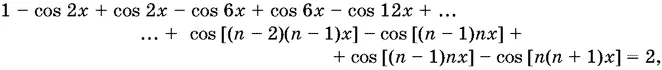
откуда

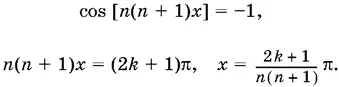
Ответ. 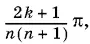где k = 0, +1, +2, ..., а натуральное n фиксировано.

13.24.Перенесем единицу в левую часть и запишем уравнение в виде

2 cos x − cos 2 x − cos² 2 x = 0,

или

2 cos x − cos 2 x (1 + cos 2 x ) = 0.

Выражение в скобках равно 2 cos² x . Поэтому

cos x (1 − cos x cos 2 x ) = 0.

Если cos x = 0, то x = π/ 2+ n π.

Если cos x cos 2 x = 1, то

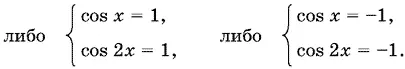
Второе уравнение первой системы преобразуется к виду 2 cos² x − 1, т. е. cos² x = 1. Следовательно, cos x = 1 и x = 2 n π.

Для второй системы аналогично получим cos² x = 0, что несовместно с первым уравнением cos x = −1.

Ответ. π/ 2+ n π; 2 n π.

13.25.Данное уравнение эквивалентно совокупности двух систем

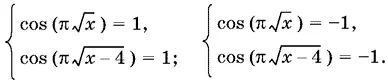
Первая система может быть переписана так:

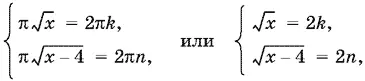
откуда

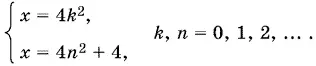
(Для k и n берутся только неотрицательные значения.) Приравнивая различные выражения для x , получим k ² = n ² + 1, откуда ( k − n )( k + n ) = 1. Так как k и n — целые и неотрицательные, то

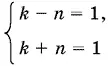
и, следовательно k = 1, n = 0.

Теперь x определяется однозначно: x = 4.

Решаем вторую систему:

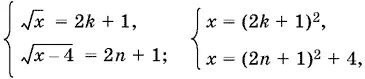
где k , n = 0, 1, 2, ... .

Приравнивая правые части последней системы, получим

(2 k + 1)² − (2 n + 1)² = 4, или ( k − n )( k + n + 1) = 1.

Так как n и k — целые и неотрицательные числа, то последнее уравнение равносильно системе

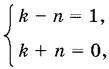
которая не имеет целых решений.

Ответ.4.

13.26.Данное уравнение можно переписать в виде

sin³ x + cos³ x = sin² x + cos² x ,

откуда

sin² x (1 − sin x ) + cos² x (1 − cos x ) = 0.

Сумма двух неотрицательных слагаемых равна нулю тогда и только тогда, когда оба слагаемых равны нулю:

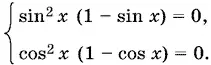
Если в первом уравнении sin x = 0, то cos x ≠ 0. Получаем систему решения которой: x = 2 k π.

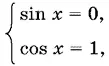
Если в первом уравнении 1 − sin x = 0, т. е. sin x = 1, то cos x ≠ 1. Приходим к системе

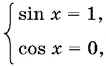
решения которой: x = π(4 k + 1)/ 2.

Ответ.2 k π; π(4 k + 1)/ 2.

13.27. Способ 1.Дополним левую часть данного уравнения до полного квадрата. Для этого придется ввести еще одно слагаемое: cos x cos 3 x , знак которого зависит от знака cos x , так как из данного уравнения следует, что cos 3 x ≥ 0.

Рассмотрим три случая.

1. Если cos x > 0, то перепишем данное уравнение в виде

cos² 3 x + ¼ cos² x − cos x cos 3 x = cos 3 x cos 4 x − cos 3 x cos x ,

или

(cos 3 x − ½ cos x )² + cos x cos 3 x (1 − cos³ x ) = 0.

В левой части стоит сумма неотрицательных выражений, следовательно,

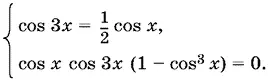
По предположению cos x > 0. Из первого уравнения последней системы следует, что тогда cos 3 x > 0. Заметим, что

1 − cos³ x = (1 − cos x )(1 + cos x + cos² x ),

причем всегда 1 + cos x + cos² x > 0. В итоге приходим к системе

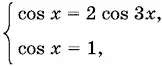
которая несовместна, так как при cos x = 1 мы получим cos 3 x = 1, а не ½.

2. Если cos x = 0, то cos 3 x = 4 cos³ x − 3 cos x = 0, и данное уравнение удовлетворяется. Получаем совокупность корней: x = π/ 2+ n π.

3. Если cos x < 0, то преобразуем уравнение к виду

(cos 3 x + ½ cos x )² + cos 3 x cos x (−1 − cos³ x ) = 0,

в котором снова оба слагаемых неотрицательны. Аналогично случаю 1, это приводит нас к несовместной системе (закончить исследование самостоятельно).

Способ 2.Уравнение можно рассматривать как квадратное относительно cos 3 x :

cos² 3 x − cos 3 x cos 4 x + ¼ cos² x = 0.

Следовательно,

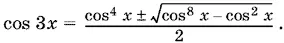
Условие cos 8 x − cos² x = cos² x (cos 6 x − 1) ≥ 0 является следствием данного уравнения. Если cos² x = 0, то x = π/ 2+ π k ; эти значения x удовлетворяют первоначальному уравнению. Если же cos² x = 1, то исходное уравнение примет вид

cos² 3 x − cos 3x + ¼ = 0, т. е. cos 3 x = ½.