Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

11.30.Пусть 3 x + 1= u , 3 y + z − x = v , тогда первые два уравнения примут вид

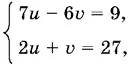
откуда u = 9, v = 9. Следовательно, x = 1, а y + z − x = 2, т. е. y + z = 3. Последнее уравнение данной системы примет теперь простой вид

lg уz = lg 2,

следствием которого будет

уz = 2.

Решаем систему

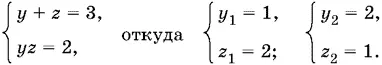
Проверкой убеждаемся, что мы нашли решения исходной системы уравнений.

Ответ.(1, 1, 2); (1, 2, 1).

12.1.В первых квадратных скобках после упрощений получим 2/ sin x , вторые квадратные скобки заключают в себе выражение 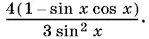Таким образом, первое слагаемое принимает вид

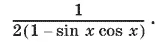
Второе слагаемое легко приводится к виду

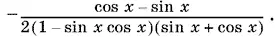
Ответ.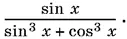

12.2.Так как сумма углов 30° − α и 60° − α равна 90° − 2α, то

tg [(30° − α) + (60° − α)] = ctg 2α,

или

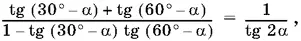
откуда следует наше тождество.

12.3.Рассмотрим выражение

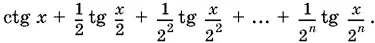
Так как ctg x = ½(ctg x / 2− tg x / 2), то

ctg x + ½ tg x / 2= ½ ctg x / 2.

Аналогичные преобразования можно продолжить и дальше:

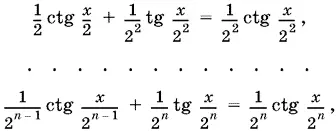
что и доказывает тождество.

12.4.Перепишем равенство

sin α cos (α + β) = sin β

в виде

sin α cos (α + β) = sin [(α + β) − α],

т. е.

sin α cos (α + β) = sin (α + β) cos α − sin α cos (α + β),

или

2 sin α cos (α + β) = sin (α + β) cos α.

Из условия следует, что cos (α + β) ≠ 0 и cos α ≠ 0. Разделим последнее равенство на cos (α + β) cos α. Получим

2 tg α = tg (α + β).

12.5.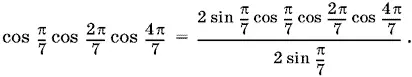

Применяя последовательно формулу синуса двойного угла, приведем числитель к виду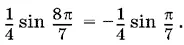

Ответ.− 1/ 8.

12.6.Вычислим вначале произведение косинусов:

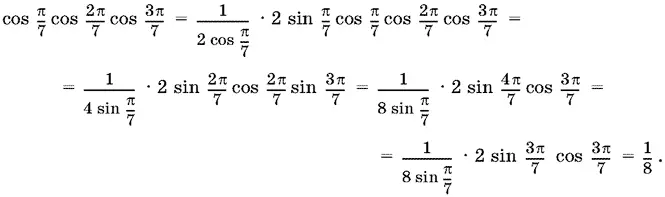
Теперь вычислим произведение квадратов синусов, умноженное на 8:

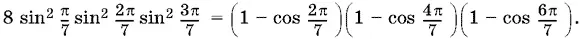
Раскроем скобки и преобразуем каждое произведение двух косинусов в сумму косинусов. После приведения подобных получим

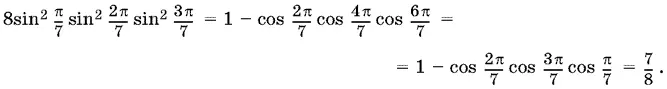
Теперь можно найти произведение тангенсов.

Ответ.√7 .

12.7.Преобразуем правую часть равенства, которое нужно доказать:

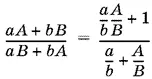
и воспользуемся условием. Получим

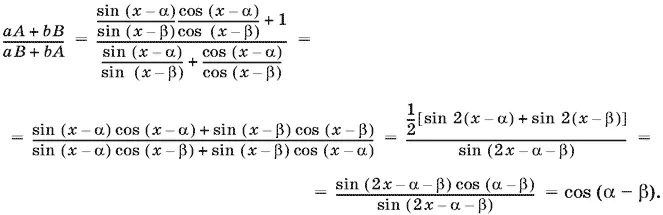
12.8.Доказательство представляет собой цепочку преобразований sin ( x + y ) sin ( x − y ) = sin² x cos² y − cos² x sin² y = k ² sin² y cos² y − cos² x sin² y = sin² y ( k ² cos² y − cos² x ).

Так как cos² x = 1 − k ² sin² y , то выражение в скобках равно k ² − 1. По условию −1 ≤ k ≤ 1, т. е. k ² − 1 ≤ 0, и, следовательно, sin ( x + y ) sin ( x − y ) ≤ 0.

12.9.Вычислим а ² + b ²:

а ² + b ² = 2 + 2 (cos α cos β + sin α sin β) = 2 + 2 cos (α − β) = 4 cos² α − β/ 2. Теперь преобразуем правую часть равенства, которое нужно доказать:

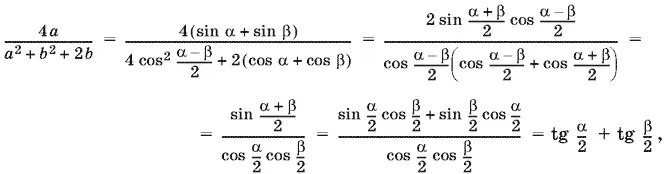
что и требовалось доказать.

12.10.Обозначим sin² α = а , sin² β = b , sin² γ = с . Тогда данное в условии соотношение примет вид

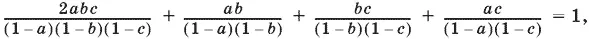
т. е.

2 abс + аb (1 − с ) + bс (1 − а ) + ас (1 − b ) − (1 − а )( а − b )(1 − с ) = 0.

После того как будут раскрыты скобки и приведены подобные члены, получим

−1 + с + b + a = 0,

что в первоначальных обозначениях соответствует равенству sin² α + sin² β + sin² γ = 1.

12.11.

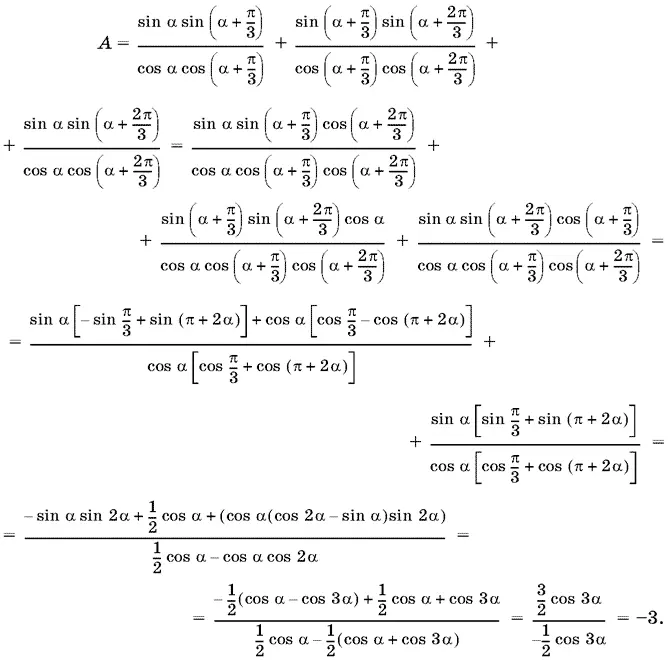
При преобразованиях мы пользовались формулами преобразования произведения тригонометрических функций в сумму.

Ответ.−3.

12.12.Так как

ctg α + ctg γ = 2 ctg β и β = π/ 2− (α + γ),

то

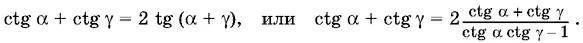
Углы α и γ острые. Поэтому ctg α > 0 и ctg γ > 0 и на их сумму можно сократить:

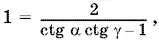
откуда легко найти произведение котангенсов.

Ответ.3.

12.13.Преобразуем данное выражение:

sin (90° + 16°) + cos (90° + 16°) ctg 8° = cos 16° − sin 16° ctg 8° = cos 16° − 2 sin 8° cos 8° cos 8°/ sin 8°= cos 16° − 2 cos² 8° = cos 16° − (1 + cos 16°) = −1.

13.1.Так как √ 2 sin ( x + π/ 4) = sin x + cos x , то

1 + sin 2 x + 2 cos 3 x sin x + 2 cos 3 x cos x = 2 sin x + 2 cos 3 x + cos 2 x .

Объединим одночлены, содержащие cos 3 x и все оставшиеся одночлены:

2 cos 3 x (sin x + cos x − 1) + 2 sin x (sin x + cos x − 1) = 0.

Получим уравнение

(sin x + cos x − 1)(cos 3 x + sin x ) = 0.

Если sin x + cos x = 1, т. е. ( x − π/ 4) = 1/ √2, то

x = n π/ 2− π/ 8и x = n π + π/ 4.

Ответ.2 n π; 2 n π + π/ 2; n π/ 2− π/ 8; n π + π/ 4.

13.2.Данное уравнение можно преобразовать так: