Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Обозначим для удобства первое основание через а , а второе через b . Оба этих основания меньше единицы. Поэтому

b < а < 1;

если x < 2, то а x > а ², b x > b ², и следовательно,

а x + b x > 1;

если же x > 2, то а x < а ², b x < b ², и следовательно, а x + b x < 1.

Ответ. x = 2.

11.9.Если x − 2 ≠ 0, 1, −1, то log 2( x + 31) = 3, x = −23. При x = 2 = 0, т. е. x = 2, имеем 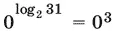, и так как log 231 > 0, то уравнение удовлетворяется.

При x − 2 = 1, т. е. x = 3, уравнение также удовлетворяется.

Если x − 2 = −1, т. е. x = 1, имеем

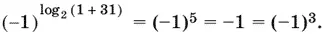
Остается проверить значение x = −23. Тогда log 28 = 3, и уравнение снова удовлетворяется.

Ответ.−23, 1, 2, 3.

11.10.Так как log 3(3 x + 1− 3) = 1 + log 3(3 x − 1), то, обозначив log 3(3 x − 1) через y , получим

y ² + y − 6 = 0,

откуда y 1= −3, y 2= 2.

Если log 3(3 x − 1) = −3, то 3 x = 28/ 27и x 1= log 328 − 3. Если log 3(3 x − 1) = 2, то 3 x = 10 и x 2= log 310.

Ответ.log 328 − 3, log 310.

11.11.Перепишем уравнение в виде

log 7 x + log x 7 = log² 7 x + log² x 7 − 7/ 4.

Дополним правую часть его до полного квадрата суммы (заметим, что log 7 x · log x 7 = 1) и обозначим

log 7 x + log x 7 = y .

Получим уравнение:

4 у ² − 4 у − 15 = 0, откуда у 1= 5/ 2, y 2= − 3/ 2.

Если log x 7 + log 7 x = 5/ 2, то

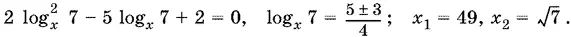
Если же log x 7 + log 7 x = − 3/ 2, то получим уравнение

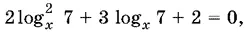
y которого нет действительных корней.

Ответ. x 1= 49, x 2= √7.

11.12.Прологарифмируем по основанию 3 и перейдем к общему основанию логарифмов:

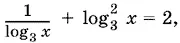
откуда следует уравнение

y ³ − 2 y + 1 = 0,

где y = log 3 x .

Так как у ³ − 2 y + 1 = ( y − 1)( y ² + y − 1), то

y 1= 1, y 2,3= −1 ± √5/ 2.

Находим соответствующие x и проверяем их.

Ответ. x 1= 3, x 2,3= 3.

11.13.Если

y = log х 3,

то придем к уравнению

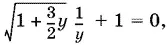
из которого получается цепочка следствий

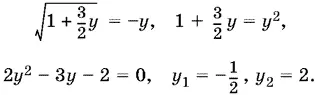
Проверкой убеждаемся, что второе значение y не удовлетворяет исходному уравнению, так как y должен быть отрицательным.

Ответ. x = 1/ 9.

11.14.Приведя уравнение к общему знаменателю и отбросив его, получим следствие данного уравнения:

log 4 x + log 4(10 − x ) = 2,

откуда

x ² − 10 x + 16 = 0, x 1= 2, x 2= 8.

Проверкой убеждаемся, что это — корни исходного уравнения.

Ответ. x 1= 2, x 2= 8.

11.15.Перепишем данное уравнение так:

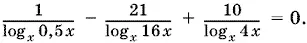
При этом преобразовании мы могли потерять корень, так как при x = 1 левая часть полученного уравнения теряет смысл, в то время как обе части исходного уравнения существуют. Проверкой убеждаемся, что x = 1 — корень данного уравнения [21] Заметим, что если бы мы перешли к основанию 2, то получили бы уравнение, равносильное данному. Убедитесь в этом самостоятельно. .

Преобразуем выражения, стоящие в знаменателях и обозначим log x 2 = y :

1/ 1 − y − 21/ 4 y + 1+ 10/ 2 y + 1= 0.

Это уравнение равносильно системе

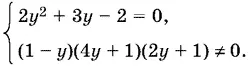
При y = −2 и y = ½, являющихся корнями уравнения, условие, входящее в систему, удовлетворяется.

Ответ. x 1= 1, x 2= 1/ √2, x 3= 4.

11.16.Перепишем уравнение в виде

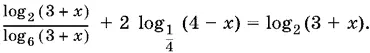
Так как

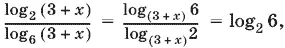
то придем к уравнению

log 26 − log 2(4 − x ) = log 2(3 + x ),

откуда

х ² − x − 6 = 0, x 1= −2, x 2= 3.

Все применявшиеся преобразования приводили к следствию исходного уравнения. Первый корень при проверке отбрасываем, так как 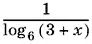при x = −2 не существует.

Ответ. x = 3.

11.17.Уравнение равносильно системе

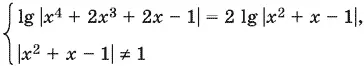
или

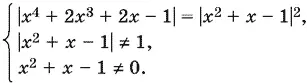
Решим уравнение, после чего проверим, выполняются ли наши ограничения. Уравнение распадается на два. Если

x 4+ 2 x ³ + 2 x − 1 = ( х ² + x − 1)²,

то, раскрывая скобки, получим

х ² + 4 x − 2 = 0, x 1,2= −2 ± √6.

Если же

x 4+ 2 x ³ + 2 x − 1 = −( х ² + x − 1)²,

то

x ²(2 x ² + 4 x − 1) = 0; x 3= 0, x 4,5= −2 ± √6/ 2.

Остается проверить выполнение двух условий, входящих в последнюю систему. Лишь при x = 0 нарушается условие | х ² + x − 1| ≠ 1. При остальных найденных значениях x оба условия выполняются.

Ответ. x 1,2= −2 ± √6; x 3,4= −2 ± √6/ 2.

11.18.Преобразуем первое слагаемое:

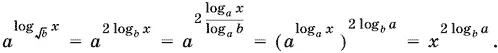
При переходе к логарифмам с основанием а мы наложили на а дополнительное ограничение: а ≠ 1. Однако при а = 1 данное нам уравнение не имеет решений, и, следовательно, такое ограничение несущественно. При замене 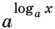на x могут быть введены посторонние корни x < 0.

Мы получили уравнение относительно :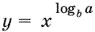

y ² − 5 у + 6 = 0; y 1= 2, y 2= 3,