Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

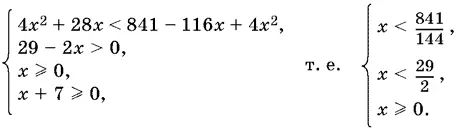
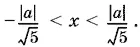
Ответ.0 ≤ x < 841/ 144.

10.26.Неравенство удобно переписать в виде

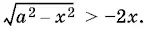
Оно равносильно совокупности двух систем

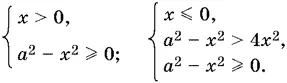
Решая последнее неравенство каждой из систем, найдем −| а | ≤ x ≤ | а |.

Так как в первой системе x > 0, то для нее получим решения:

0 < x ≤ | а |, а ≠ 0.

Перейдем ко второй системе. Решая второе неравенство, получим

− | а |/ √5 < x < | а |/ √5.

Мы приходим к системе

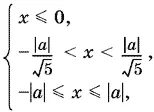
решениями которой будут значения из интервала − | а |/ √5 < x ≤ 0 при а ≠ 0. Остается объединить решения двух систем.

Ответ.При а ≠ 0: − | а |/ √5< x ≤ | а |; при а = 0 неравенство не имеет решений.

10.27.Приведем степени, входящие в данное неравенство, к основанию 2 и поделим на 2 √ x 2 x :

2 x − √ x ≤ 3 + 4 · 2 √ x − x ;

обозначив 2 x − √ x = y, получим

y ≤ 3 + 4/ y ,

а так как y > 0, то

y ² − 3y − 4 ≤ 0.

Корни трехчлена: −1, 4; так как меньший корень отрицателен, то получаем

2 x − √ x ≤ 4,

т. е. x − √ x ≤ 2. Обозначим √ x = z и найдем решения неравенства

z ² − z − 2 ≤ 0.

Получим −1 ≤ z ≤ 2. Левое неравенство выполняется, если только √ x существует. Остается √x ≤ 2, т. е. 0 ≤ x ≤ 4.

Ответ.0 ≤ x ≤ 4.

10.28.Перепишем неравенство в виде

3 √ x (3 + x − 2 x ²) − 2(−2 x ² + x + 3) < 0,

или

(3 √ x − 2)(−2 x ² + x + 3) < 0.

Последнее неравенство [20] Хотя метод интервалов был изложен во введении применительно к многочленам, им можно пользоваться при решении более широкого класса неравенств. В частности, для этого неравенства получаем (3 √ x − 2)( x + 1)( x − 3 / 2 ) >0. Первый множитель обращается в нуль при причем он больше нуля при и меньше нуля при Нанесем точки −1, и 3 / 2 на числовую ось и воспользуемся тем обстоятельством, что при x > 3 / 2 все три скобки положительны. Так как, кроме того, x ≥ 0, окончательно получим равносильно совокупности систем

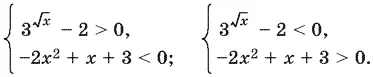
Решая первую систему, получим

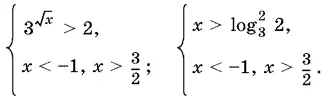
Так как −1 < 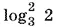< 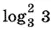= 1 < 3/ 2, то окончательно получим x > 3/ 2.

Вторая система дает нам следующее:

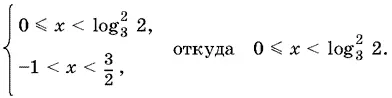
Ответ.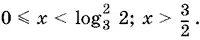

10.29.Если x > 0, то неравенство равносильно такому:

( x − 1)2 x − 1/ 3 − x < 0, т. е. ( x − 1)( x − ½)/ x − 3> 0.

Воспользовавшись методом интервалов, получим ½ < x < 1, x > 3. Если x = 0, то левая часть неравенства обращается в выражение 0 −⅓, которое не имеет смысла.

При x < 0 показатель степени должен быть целым числом, т. е. 2 x − 1/ 3 − x , откуда x (2 + n ) = 3 n + 1. Так как при n = −2 последнее уравнение не удовлетворяется, то

x = 3 n + 1/ 2 + n .

Из условия x < 0 находим x = 3 n + 1/ 2 + n < 0 и, следовательно, −2 < n < −⅓. Единственное целое число в этом интервале n = −1, а соответствующее ему значение неизвестного x = −2. Проверяем это значение, подставляя его в первоначальное неравенство: (−2) −1< 1.

Ответ. x = −2, ½ < x < 1, x > 3.

10.30.Предположим, что основание больше единицы, т. е. 4 x ² + 12 x + 10 > 1, или (2 x + 3)² > 0. Это имеет место при всех x , кроме x = − 3/ 2. При x = − 3/ 2основание равно единице, и, следовательно, исходное неравенство удовлетворяется. Если же x ≠ − 3/ 2, то оно равносильно неравенству

| х ³ − 5 х + 2| ≥ x − 2,

которое заведомо удовлетворяется при x − 2 ≤ 0, т. е. при x ≤ 2. Пусть теперь x > 2. Разложим трехчлен на множители:

| х ³ − 5 х + 2| = | х ³ − 4 x − ( x − 2)| = | x − 2| | х ² + 2 x − 1| = ( x − 2)| х ² + 2 x − 1|.

Так как x > 2, то получаем равносильное неравенство

| х ² + 2 x − 1| ≥ 1,

а поскольку x ² + 2 x − 1 = x ² + 2( x − ½) > 0, то

х ² + 2 x − 1 ≥ 1, или x ² + 2( x − 1) ≥ 0.

Последнее неравенство удовлетворяется при любом x > 2.

Ответ. x − любое действительное число.

10.31.Так как x > 0, то вместо неравенства

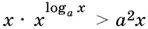
можно написать

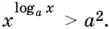
Если а > 1, то при логарифмировании по основанию а знак неравенства не изменится:

(log аx )² > 2,

откуда log ax < −√2, log a x > √2, т. е.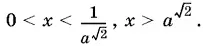

Если 0 < а < 1, то (log a x )² < 2 и

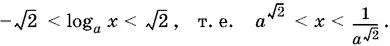
Ответ.При 0 < a < 1, 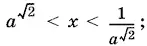при а > 1, 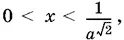x > a √2.

10.32.Если x > 0, то получаем неравенство, равносильное данному:

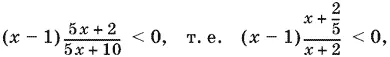
откуда 0 < x < 1.

Значение x = 0 удовлетворяет исходному неравенству. Если же x < 0, то непременно

5 x + 2/ 5 x + 10= n ,