Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Подкоренное выражение можно преобразовать следующим образом:

(1 − а ² + b ²)² − 4 b ² = (1 − а ² + b ² − 2 b )(1 − а ² + b ² + 2 b ) = [(1 − b )² − а ²][(1 + b )² − а ²] = (1 − b − а )(1 − b + а )(1 + b − а )(1 + b + а ).

Так как а > b > 0 и а + b < 1, то каждый из четырех множителей положителен и дискриминант тоже положителен.

Если перед корнем выбран знак плюс, то u и v положительны. Докажем, что v > 0. Имеем а ² − b ² = ( а − b )( а + b ) < а − b < а − b + 2 b = а + b < 1. Следовательно, 1 − а ² + b ² > 0 и, обращаясь к выражению для v , находим, что v > 0. Так как а > b , то очевидно, что и u > 0.

Если перед корнем выбран знак минус, то нужно проверить, что u и v положительны. Так как а > b , то проверку достаточно провести для v , которое меньше u .

Неравенство 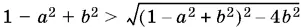очевидно.

Нетрудно проследить, что в процессе решения системы уравнений относительно u и v при условии, что u и v положительны, мы не нарушали равносильности.

Способ 2.Эту систему естественно было бы решать с помощью подстановки x = sin φ, y = sin ψ, где 0 < φ < π/ 2, 0 < ψ < π/ 2. Такая подстановка возможна, поскольку из имеющихся в условии ограничений легко получить, что 0 < x < 1, 0 < y < 1. Получим систему

Складывая и вычитая уравнения этой системы, найдем

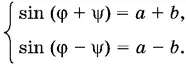
Так как по условию 0 < а + b < 1 и 0 < а − b < 1, а на φ и ψ были наложены ограничения 0 < φ < π/ 2, 0 < ψ < π/ 2, то можно написать

или

Из первой системы получим

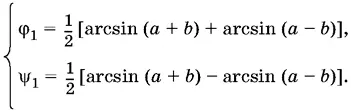
Найдем sin φ 1и sin ψ 1:

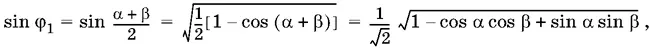
где α = arcsin ( а + b ), β = arcsin ( а − b ). (При выборе знаков перед корнями мы здесь и в дальнейшем принимаем во внимание ограничения на φ и ψ: 0 < φ < π/ 2, 0 < ψ < π/ 2.) Продолжим преобразования:

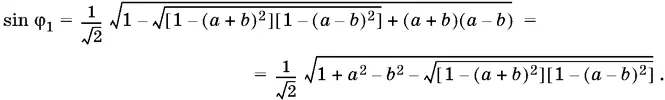
Нетрудно убедиться в том, что

[1 − ( а + b )²][1 − ( а − b )²] = (1 − а ² + b ²)² − 4 b ².

Аналогично найдем sin ψ 1 ,а также sin φ 2и sin ψ 2.

Ответ.Если а > b > 0, а + b < 1, то система имеет два решения:

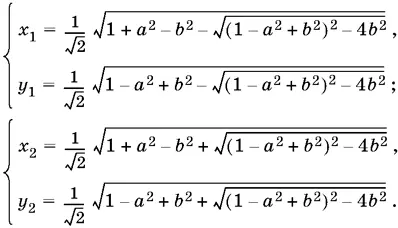
9.30.Наряду с решением x 1, y 1, z 1система обязательно имеет решение − х 1, − у 1, z 1. Поэтому у системы будет единственное решение только в том случае, когда x = y = 0.

Подставляя x = y = 0 в исходную систему, получим

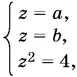
откуда либо а = b = 2, либо а = b = −2.

Проверим, действительно ли при найденных значениях а и b система имеет единственное решение.

Если а = b = 2, то из первого уравнения находим

xyz = 2 − z .

Подставляя во второе, получим квадратное уравнение относительно z :

z ² − 3 z + 2 = 0,

корни которого z 1= 1, z 2= 2.

При z = 1 получим систему

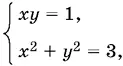
которая, как легко проверить, имеет четыре решения.

Таким образом, значения параметров а = b = 2 не удовлетворяют условию задачи.

Если а = b = −2, то из первого уравнения найдем

xyz = −2 − z .

Подставляем во второе:

z ² + z − 2 = 0,

откуда z 1= −2, z 2= 1.

При z = −2 приходим к системе

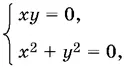
имеющей единственное решение x = y = 0. При z = 1 получаем систему

Подставляем во второе уравнение y = − 3/ x и убеждаемся, что уравнение x 4− 3 x ² + 9 = 0, которое получается в результате, имеет только мнимые корни.

Ответ. a = b = −2.

9.31.По условию y = − x . Данные уравнения примут вид

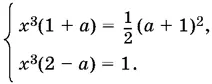
Если а ≠ −1, то, найдя x ³ из первого и второго уравнений, приравняем полученные выражения

½( а + 1) = 1/ 2 − a , т. е. а ² − а = 0,

откуда а = 0 или а = 1.

Условию задачи могут удовлетворить только три значения параметра а :

−1, 0, 1,

которые нужно проверить.

Если а = −1, то из первого уравнения найдем y = − x , а из второго уравнения найдем x ³ = ⅓ и 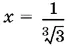, а следовательно, 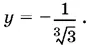Найденные значения неизвестных удовлетворяют и условию x + y = 0.

Если а = 0, то из первого уравнения: 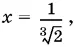а из второго: 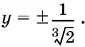Это значит, что при а = 0 система имеет два решения:

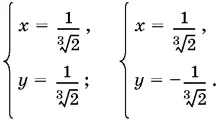
По условию любое решение должно удовлетворять требованию x + y = 0, между тем первое решение этому требованию не удовлетворяет. Значение а = 0 мы должны отбросить.

Осталось рассмотреть случай, когда а = 1. B этом случае получим систему

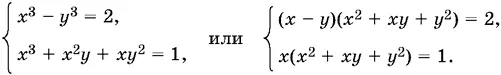
Так как правые части отличны от нуля, то разделим первое уравнение на второе, откуда x + y = 0. Поскольку условие x + y = 0 теперь автоматически выполняется для любого решения системы, то нужно убедиться, что y этой системы есть хотя бы одно решение. Таким решением является x = 1, y = −1. (Докажите.)