Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.Неабсолютное тождество. Область определения левой части: x ≠ π/ 2+ k π, область определения правой части: x ≠ k π/ 2.

4—6.Тождество 4 является абсолютным, поскольку это определение секанса. Тождества 5 и 6 неабсолютные, так как правые части определены всегда, в то время как левые могут терять смысл.

7—8.Тождество 7 абсолютное. B самом деле, левая часть теряет смысл при cos x / 2= 0. Правая часть может быть записана в виде 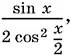т. е. тоже теряет смысл при cos x / 2= 0.

Тождество 8 неабсолютное. Левая часть теряет смысл при cos x / 2= 0, а правая, которая может быть записана в виде 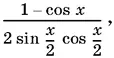перестает существовать как при cos x / 2= 0, так и при sin x / 2= 0.

9—10.Левую часть равенства 9 можно преобразовать так:

ctg 2 x = cos 2 x / sin 2 x = cos 2 x / 2sin x cos x ,

а правую записать в виде

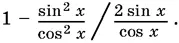
Обе части этого равенства перестают существовать одновременно, если либо cos x = 0, либо sin x = 0, следовательно, тождество 9 абсолютное.

Тождество 10 является неабсолютным, поскольку при x = π/ 2(2 n + 1) левая часть равна нулю, а правая теряет смысл.

11—13.Первое из этих трех тождеств неабсолютное, второе и третье — абсолютные.

14—16.Первое и второе тождества неабсолютные, третье — абсолютное.

B самом деле, для первого область определения левой части: x > 0, y > 0; x < 0, y < 0, а область определения правой части: x ≠ 0; y ≠ 0. Для второго область определения левой части x ≠ 0, а область определения правой части x > 0.

Наконец, для третьего x ≠ 0 для обеих частей тождества.

17.Пусть x = а — корень данного уравнения. Тогда f ( а ) = φ( а ). Поскольку ψ( x ) существует при всех x , то ψ( а ) — число; следовательно,

f ( a ) + ψ( а ) = φ( а ) + ψ( а ). (1)

Таким образом, x = а — корень уравнения

f ( x ) + ψ( x ) = φ( x ) + ψ( x ). (2)

Обратно: если x = а — корень (2), то имеет место равенство (1), а потому x = а — корень уравнения f ( x ) = φ( x ).

Вторую часть теоремы доказывает пример. B самом деле, достаточно рассмотреть два уравнения:

x − 1 = 0 и x − 1 + 1/ x − 1 = 1/ x − 1,

первое из которых имеет единственный корень x = 1, а второе вовсе не имеет корней, так как при x = 1 оно теряет смысл.

18.Доказательство аналогично 17. Даже пример можно взять тот же самый.

19—19а.Для доказательства достаточно заметить, что посторонними для данного уравнения могут быть те корни уравнения

f ( x ) = ψ( x ),

для которых φ( x ) либо не существует, либо обращается в нуль.

20.Если f ( а ) = φ( а ), то [ f ( а )]² = [φ( а )]². Обратно: из второго равенства следует, что либо f ( а ) = φ( а ), либо f ( а ) = −φ( а ).

21.Система равносильна совокупности четырех систем:

22.Доказательство непосредственно следует из свойств пропорций.

9.1.При x < −2 получим

− x + 2 x + 2 − 3 x − 6 = 0,

т. е. x = −2, что противоречит предположению. Таким образом, при x < −2 уравнение не имеет решений.

При −2 ≤ x ≤ −1 получим x = −2.

При −1 < x ≤ 0 уравнение обращается в ложное числовое равенство 4 = 0. На этом интервале нет решений.

Наконец, при x > 0 получаем x = −2, что снова противоречит ограничению.

Ответ. x = −2.

9.2.Пусть x ² = y . Тогда

| y − 9| + | y − 4| = 5.

Точки y = 4 и y = 9 разбивают числовую ось на три интервала.

Если y < 4, уравнение примет вид

9 − y + 4 − y = 5,

откуда y = 4. Это значение не принадлежит выбранному интервалу.

Если 4 ≤ y ≤ 9, то знаки абсолютной величины следует раскрыть так:

9 − y + y − 4 = 5, т. е. 5 = 5.

Так как уравнение обратилось в верное числовое равенство, то все значения y из интервала 4 ≤ y ≤ 8 являются решениями.

При y > 9 получим

y − 9 + y − 4 = 5,

т. е. y = 9. Здесь снова нет решений. Вспоминая, что y = x ², запишем

4 ≤ x ² ≤ 9, или 2 ≤ | x | ≤ 3.

Ответ.−3 ≤ x ≤ −2; 2 ≤ x ≤ 3.

9.3. Способ 1.Дополним стоящую слева сумму квадратов до полного квадрата:

( x − 3 x / 3 + x )² + 6 x ²/ 3 + x − 7 = 0,

т. е.

( x ²/ 3 + x )² + 6 x ²/ 3 + x − 7 = 0,

откуда получаем совокупность уравнений:

x ²/ 3 + x = −7, x ²/ 3 + x = 1.

Действительных решений y этой совокупности уравнений нет.

Способ 2.Введем новое неизвестное:

3 x / 3 + x = u , или 3 x = 3 u + xu .

Получим систему

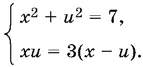
Вычитая из первого уравнения удвоенное второе, придем к уравнению относительно x − u

( x − u )² + 6( x − u ) − 7 = 0, откуда следует совокупность двух уравнений:

x − u = −7, x − u = 1.

Решая каждое из этих уравнений, убедимся, что действительных корней нет.

Ответ.Решений нет.

9.4.Возведем данное уравнение в куб:

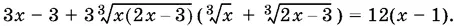
Стоящий в скобках в левой части уравнения двучлен заменим правой частью данного уравнения и приведем подобные члены:

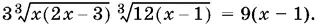
Такая замена может привести к появлению посторонних корней. B самом деле, при возведении а + b = с в куб мы получаем равенство, справедливое при всех тех же значениях а , b и с , что и данное равенство. После замены же мы получим

а ³ + b ³ + 3 аbс = с ³.

Это равенство удовлетворяется при а = b = 1, с = −1, в то время как исходное равенство а + b = с при этих значениях букв ложно. Следовательно, мы должны завершить решение проверкой.